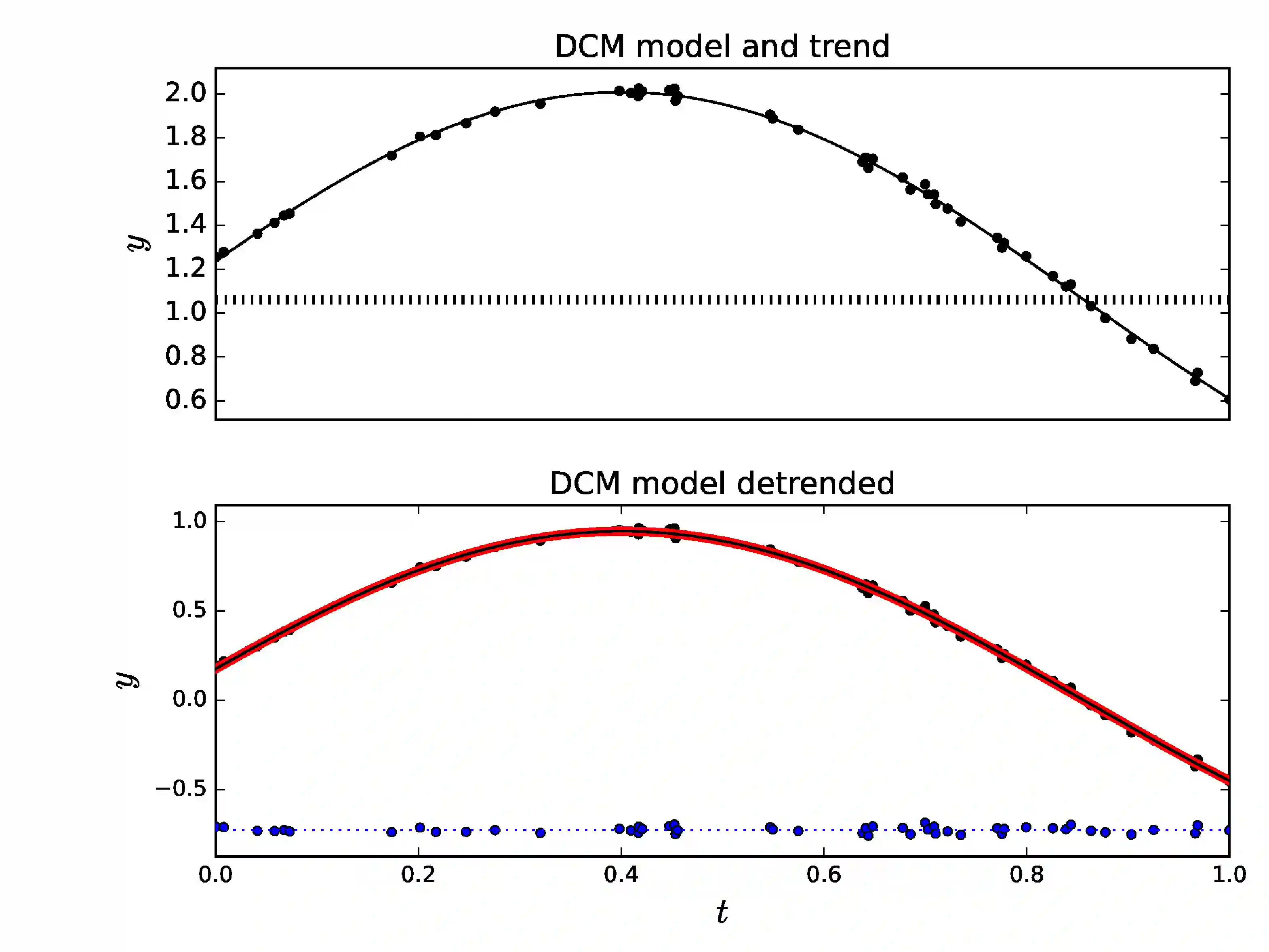
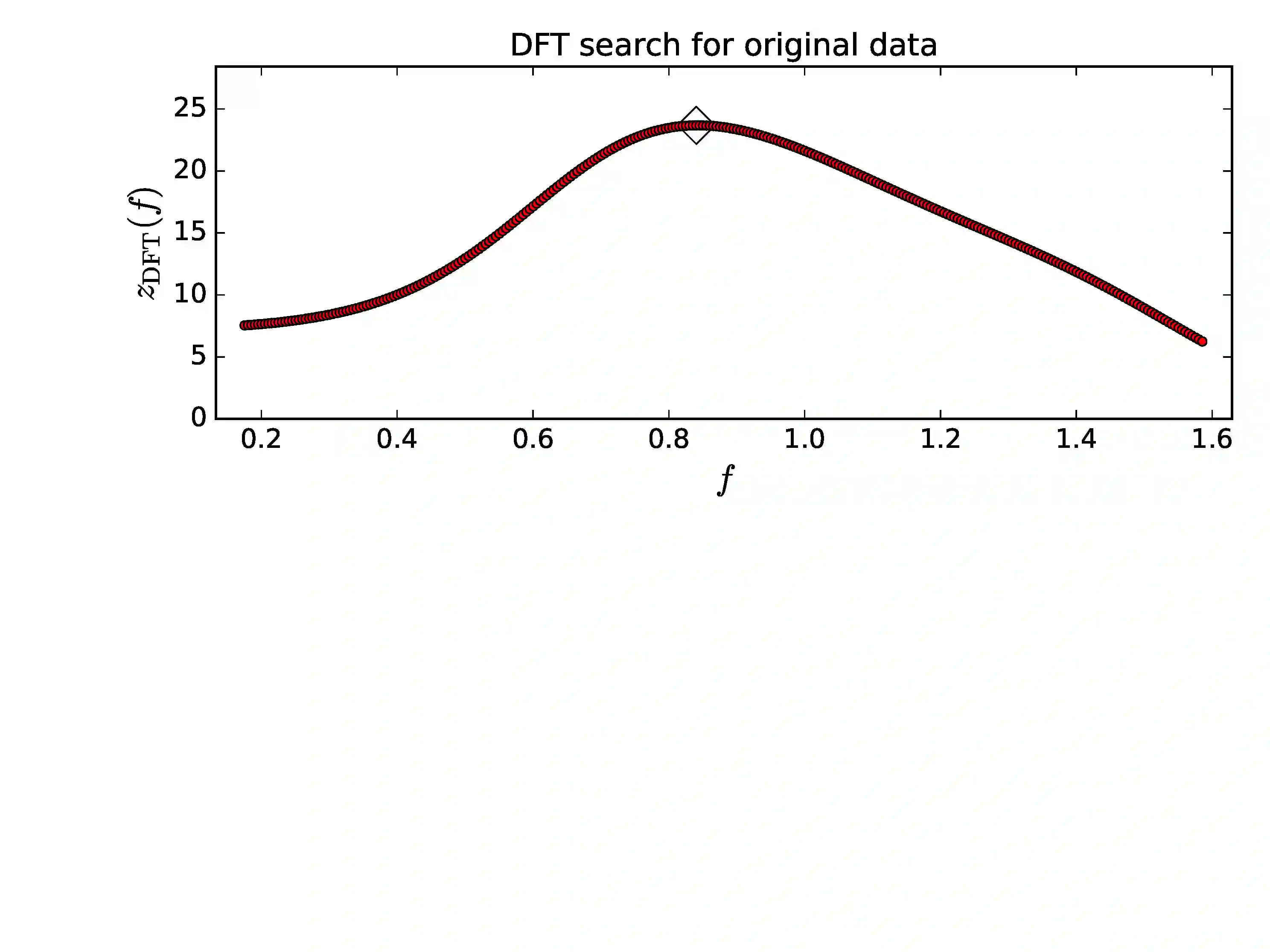
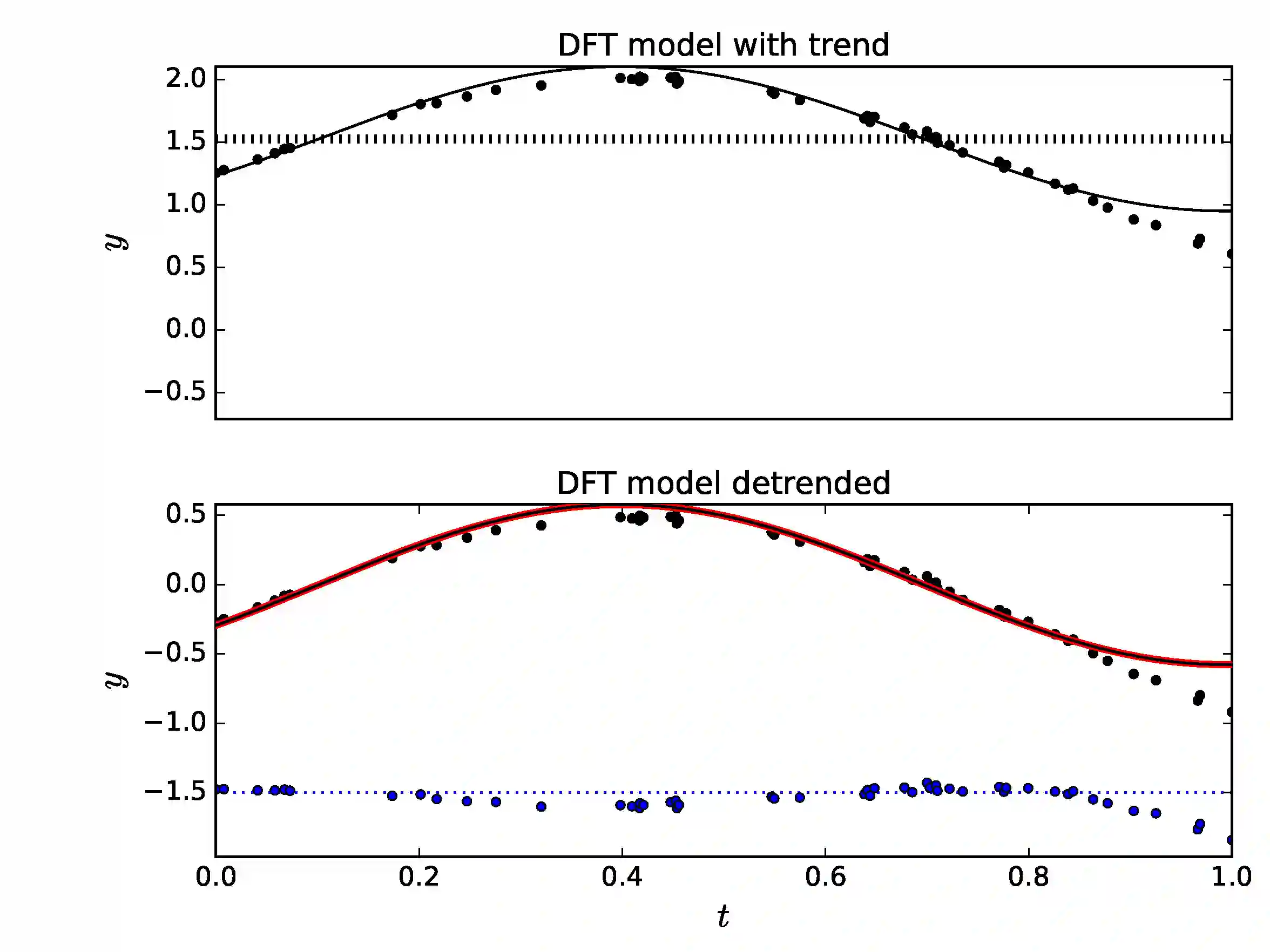
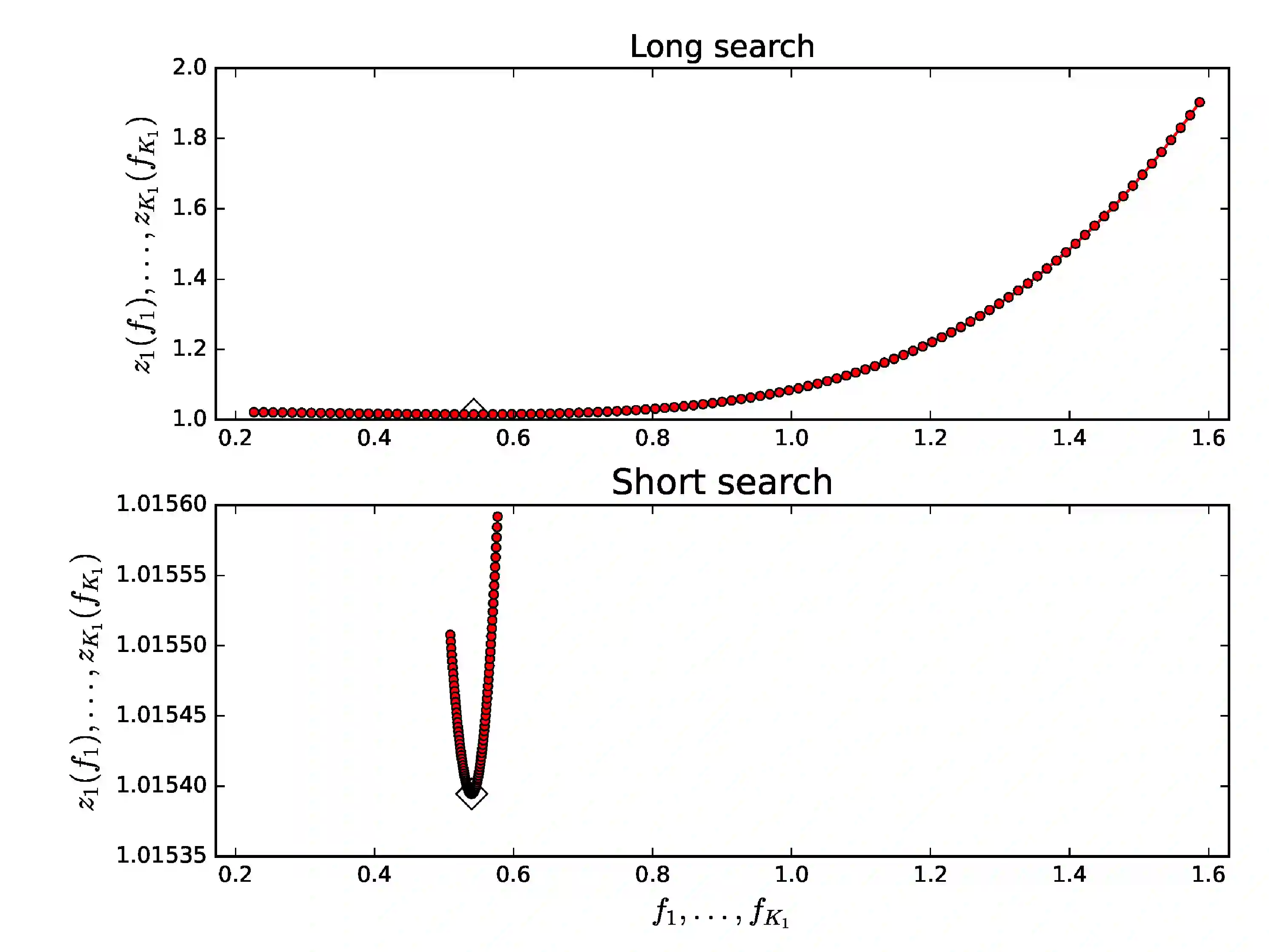
离散傅里叶变换与离散卡方方法对比 (Discrete Fourier Transform versus Discrete Chi-Square Method)

We compare two time series analysis methods, the Discrete Fourier Transform (DFT) and our Discrete Chi-square Method (DCM). DCM is designed for detecting many signals superimposed on an unknown trend. The solution for the non-linear DCM model is an ill-posed problem. The backbone of DCM is the Gauss-Markov theorem that the least squares fit is the best unbiased estimator for linear regression models. DCM is a simple numerical time series analysis method that performs a massive number of linear least squares fits. Hence, the data spacing, even or uneven, is irrelevant. We show that our numerical solution for the DCM model fulfils the three conditions of a well-posed problem: existence, uniqueness and stability.The Fisher-test is used to identify the best DCM model from all alternative tested DCM models. The correct DCM model must also pass our Predictivity-test. Our analyses of seven different simulated data samples expose the weaknesses of DFT and the efficiency of DCM. The DCM signal and trend detection depend only on the sample size and the accuracy of data. DCM is an ideal forecasting method because the time span of observations is irrelevant. If the Gauss-Markov theorem is valid, DCM can not fail. We recommend fast sampling of large high quality datasets and the analysis of those datasets using numerical DCM parallel computation Python code.

翻译：我们比较了两种时间序列分析方法：离散傅里叶变换（DFT）与我们提出的离散卡方方法（DCM）。DCM 旨在检测叠加在未知趋势上的多个信号。非线性 DCM 模型的求解是一个不适定问题。DCM 的核心基于高斯-马尔可夫定理，即最小二乘拟合是线性回归模型的最佳无偏估计量。DCM 是一种简单的数值时间序列分析方法，它执行大量线性最小二乘拟合。因此，数据间隔（均匀或非均匀）无关紧要。我们证明了 DCM 模型的数值解满足适定问题的三个条件：存在性、唯一性和稳定性。Fisher 检验用于从所有备选测试的 DCM 模型中识别最佳 DCM 模型。正确的 DCM 模型还必须通过我们的可预测性检验。我们对七个不同模拟数据样本的分析揭示了 DFT 的弱点与 DCM 的效率。DCM 的信号与趋势检测仅取决于样本量和数据精度。DCM 是一种理想的预测方法，因为观测的时间跨度无关紧要。若高斯-马尔可夫定理成立，DCM 不可能失效。我们建议对大样本高质量数据集进行快速采样，并使用数值 DCM 并行计算 Python 代码分析这些数据集。