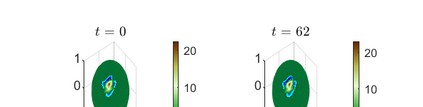
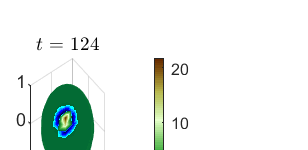
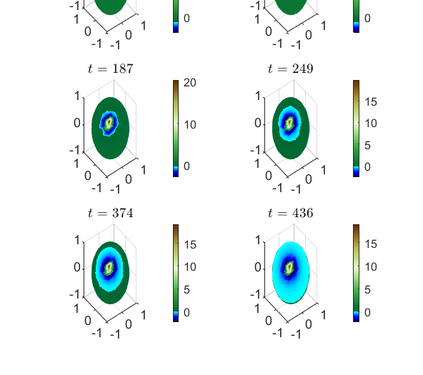
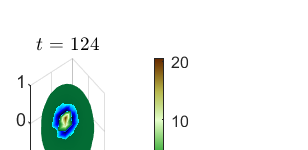
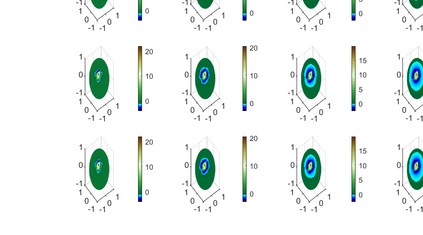
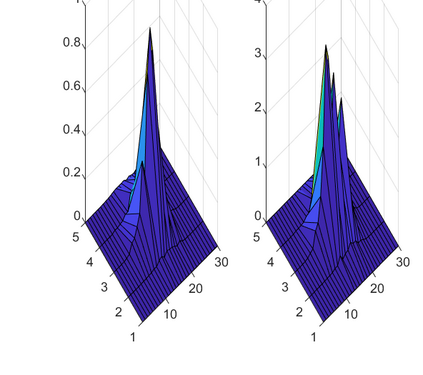
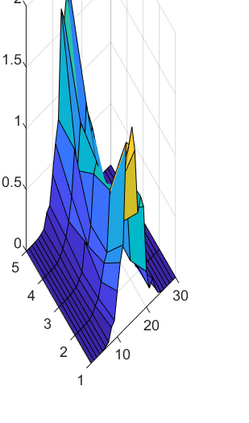
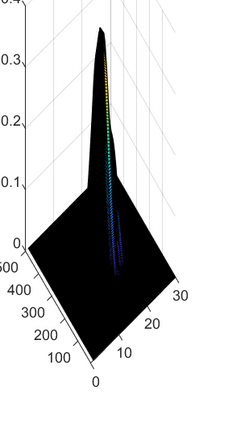
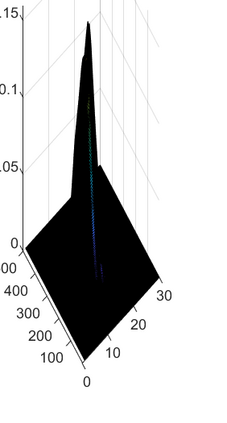
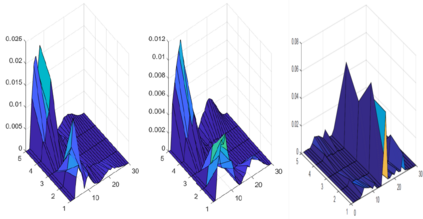
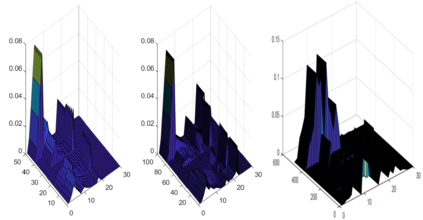
This paper considers the problem of manifold functional multiple regression with functional response, time--varying scalar regressors, and functional error term displaying Long Range Dependence (LRD) in time. Specifically, the error term is given by a manifold multifractionally integrated functional time series (see, e.g., Ovalle--Mu\~noz \& Ruiz--Medina, 2024)). The manifold is defined by a connected and compact two--point homogeneous space. The functional regression parameters have support in the manifold. The Generalized Least--Squares (GLS) estimator of the vector functional regression parameter is computed, and its asymptotic properties are analyzed under a totally specified and misspecified model scenario. A multiscale residual correlation analysis in the simulation study undertaken illustrates the empirical distributional properties of the errors at different spherical resolution levels.
翻译:暂无翻译