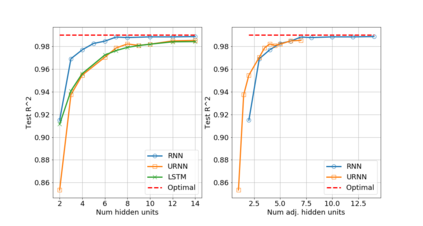
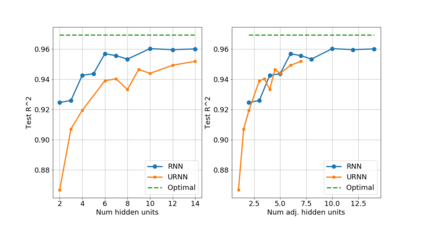
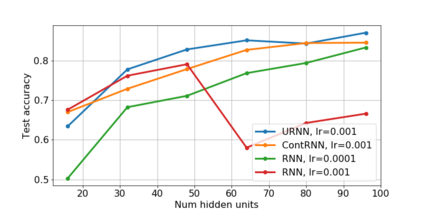
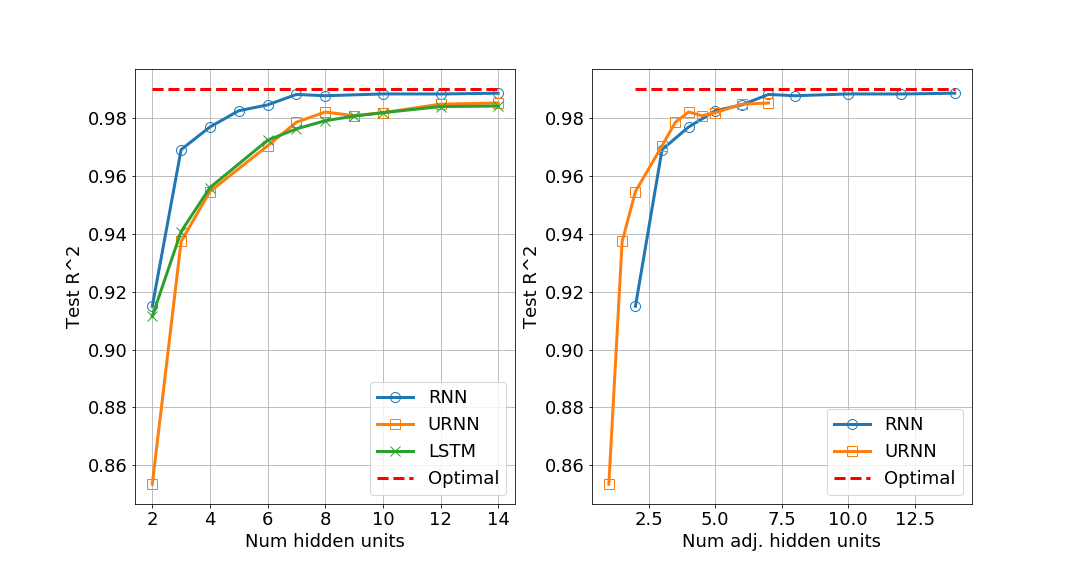
Unitary recurrent neural networks (URNNs) have been proposed as a method to overcome the vanishing and exploding gradient problem in modeling data with long-term dependencies. A basic question is how restrictive is the unitary constraint on the possible input-output mappings of such a network? This work shows that for any contractive RNN with ReLU activations, there is a URNN with at most twice the number of hidden states and the identical input-output mapping. Hence, with ReLU activations, URNNs are as expressive as general RNNs. In contrast, for certain smooth activations, it is shown that the input-output mapping of an RNN cannot be matched with a URNN, even with an arbitrary number of states. The theoretical results are supported by experiments on modeling of slowly-varying dynamical systems.
翻译:提出合并的中枢神经网络(URNNs)是克服长期依赖数据模型中渐变和爆炸的梯度问题的一种方法。一个基本的问题是,对此种网络可能的输入-输出映射的单一限制是多大的限制性?这项工作表明,对于使用RELU激活的任何合同性 RNN 来说,有一个URN,其隐藏状态最多是隐藏状态的两倍,输入-输出映射相同。因此,随着RELU的激活,URNs与一般的RNS一样具有表达性。相比之下,对于某些平稳的激活而言,一个RNNN的输入-输出映射无法与URNN相匹配,即使有任意数量的国家。理论结果得到缓慢变化的动态系统模型实验的支持。