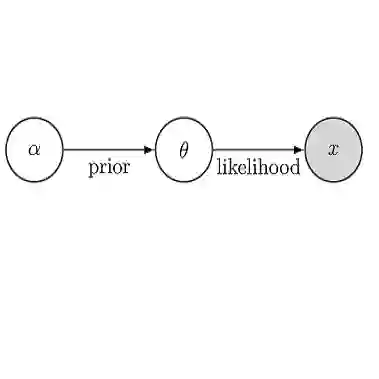
Generalized linear models (GLMs) are routinely used for modeling relationships between a response variable and a set of covariates. The simple form of a GLM comes with easy interpretability, but also leads to concerns about model misspecification impacting inferential conclusions. A popular semi-parametric solution adopted in the frequentist literature is quasi-likelihood, which improves robustness by only requiring correct specification of the first two moments. We develop a robust approach to Bayesian inference in GLMs through quasi-posterior distributions. We show that quasi-posteriors provide a coherent generalized Bayes inference method, while also approximating so-called coarsened posteriors. In so doing, we obtain new insights into the choice of coarsening parameter. Asymptotically, the quasi-posterior converges in total variation to a normal distribution and has important connections with the loss-likelihood bootstrap posterior. We demonstrate that it is also well-calibrated in terms of frequentist coverage. Moreover, the loss-scale parameter has a clear interpretation as a dispersion, and this leads to a consolidated method of moments estimator.
翻译:暂无翻译