$C^1$-conforming variational discretization of the biharmonic wave equation

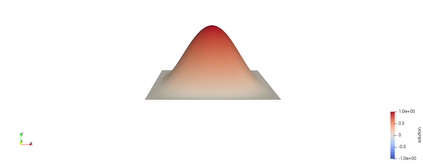
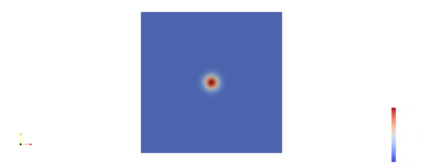
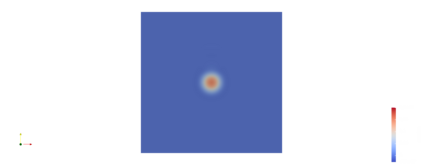
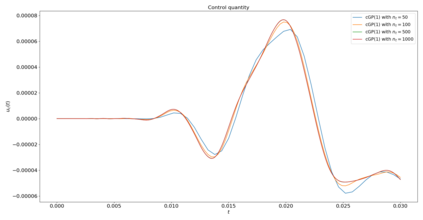
Biharmonic wave equations are of importance to various applications including thin plate analyses. In this work, the numerical approximation of their solutions by a $C^1$-conforming in space and time finite element approach is proposed and analyzed. Therein, the smoothness properties of solutions to the continuous evolution problem is embodied. High potential of the presented approach for more sophisticated multi-physics and multi-scale systems is expected. Time discretization is based on a combined Galerkin and collocation technique. For space discretization the Bogner--Fox--Schmit element is applied. Optimal order error estimates are proven. The convergence and performance properties are illustrated with numerical experiments.