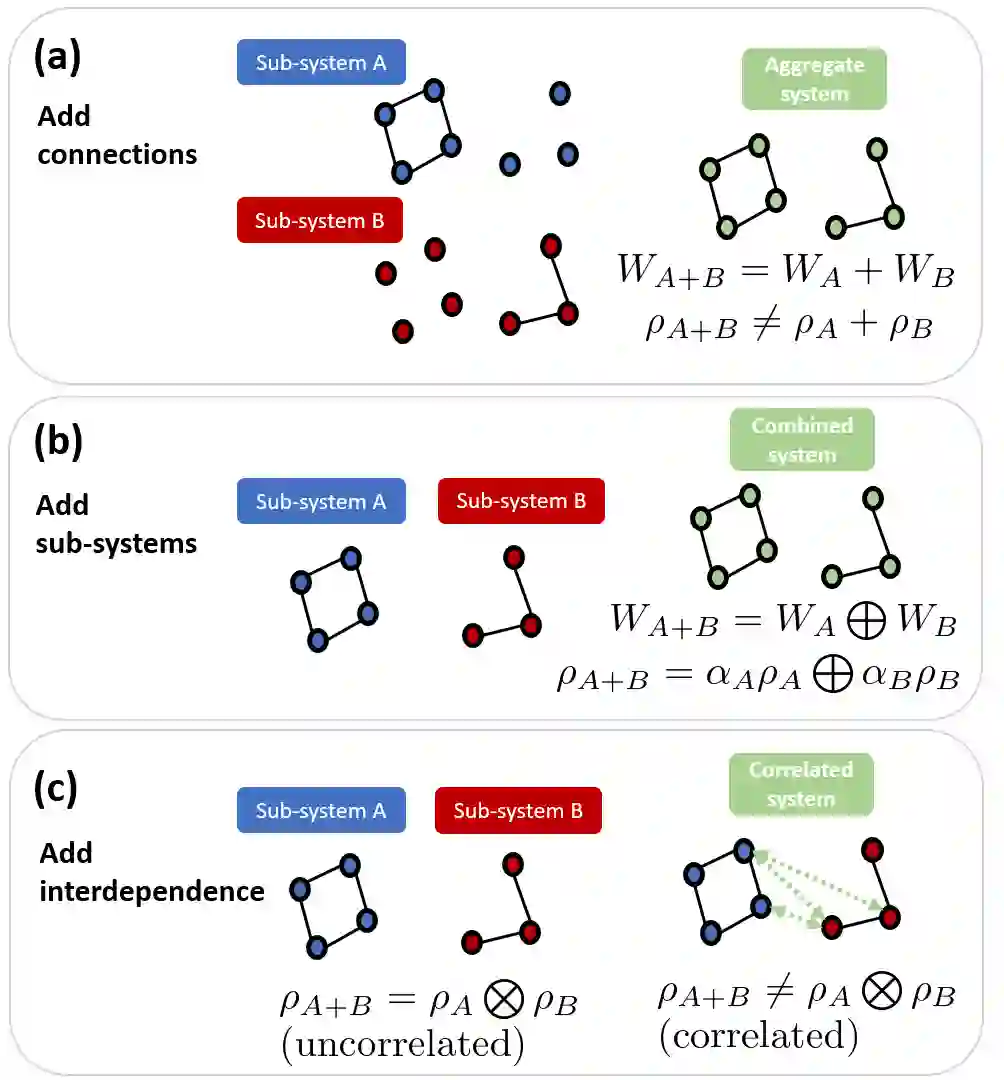
Complex network states are characterized by the interplay between system's structure and dynamics. One way to represent such states is by means of network density matrices, whose von Neumann entropy characterizes the number of distinct microstates compatible with given topology and dynamical evolution. In this Letter, we propose a maximum entropy principle to characterize network states for systems with heterogeneous, generally correlated, connectivity patterns and non-trivial dynamics. We focus on three distinct coalescence processes, widely encountered in the analysis of empirical interconnected systems, and characterize their entropy and transitions between distinct dynamical regimes across distinct temporal scales. Our framework allows one to study the statistical physics of systems that aggregate, such as in transportation infrastructures serving the same geographic area, or correlate, such as inter-brain synchrony arising in organisms that socially interact, and active matter that swarm or synchronize.
翻译:复杂网络国家的特征是系统结构和动态之间的相互作用。 代表这种状态的一种方法是网络密度矩阵,该矩阵的 von Neumann entropy 描述与特定地形和动态演变相容的不同微国家的数量。在本信中,我们提出了一个最大限度的恒星原则,以描述具有多种、普遍关联、连通模式和非三角动态的系统的网络状态。我们侧重于三个不同的联结过程,这些过程在分析实验性互联系统时广泛遇到,并描述其酶特征和不同时间尺度不同动态系统之间的转变。 我们的框架允许研究综合系统的统计物理学,例如为同一地理区域服务的运输基础设施,或相关关系,如在社会互动的有机体中产生的脑间同步以及动态物质或同步或同步的动态物质。