Differential recurrences for the distribution of the trace of the $β$-Jacobi ensemble

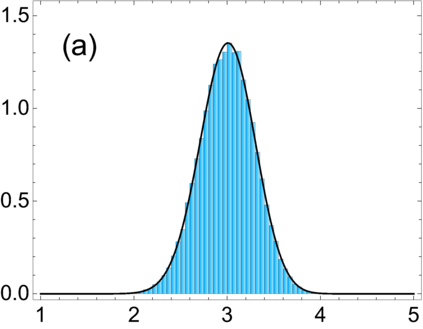
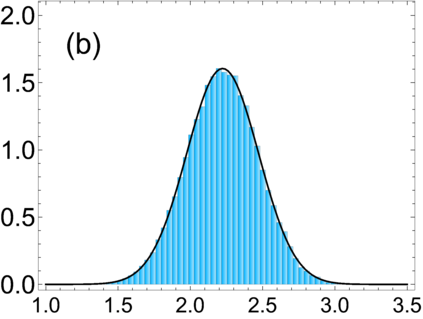
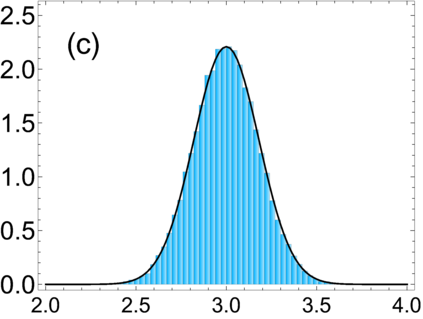
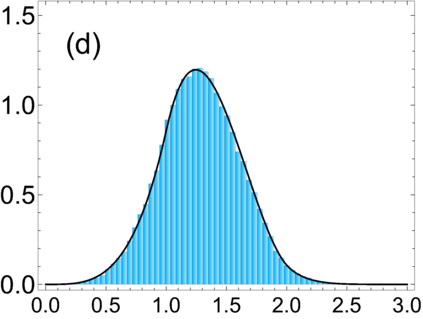
Examples of the $\beta$-Jacobi ensemble specify the joint distribution of the transmission eigenvalues in scattering problems. In this context, there has been interest in the distribution of the trace, as the trace corresponds to the conductance. Earlier, in the case $\beta = 1$, the trace statistic was isolated in studies of covariance matrices in multivariate statistics, where it is referred to as Pillai's $V$ statistic. In this context, Davis showed that for $\beta = 1$ the trace statistic, and its Fourier-Laplace transform, can be characterised by $(N+1) \times (N+1)$ matrix differential equations. For the Fourier-Laplace transform, this leads to a vector recurrence for the moments. However, for the distribution itself the characterisation provided was incomplete, as the connection problem of determining the linear combination of Frobenius type solutions that correspond to the statistic was not solved. We solve this connection problem for Jacobi parameter $b$ and Dyson index $\beta$ non-negative integers. For the other Jacobi parameter $a$ also a non-negative integer, the power series portion of each Frobenius solution terminates to a polynomial, and the matrix differential equation gives a recurrence for their computation.