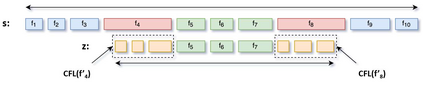
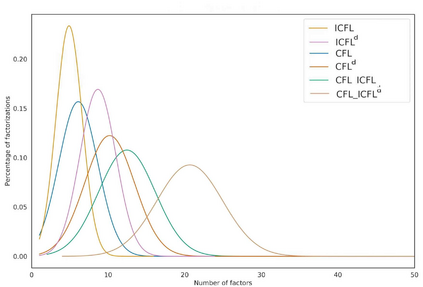
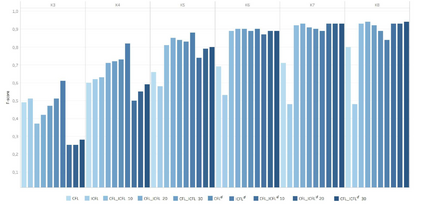
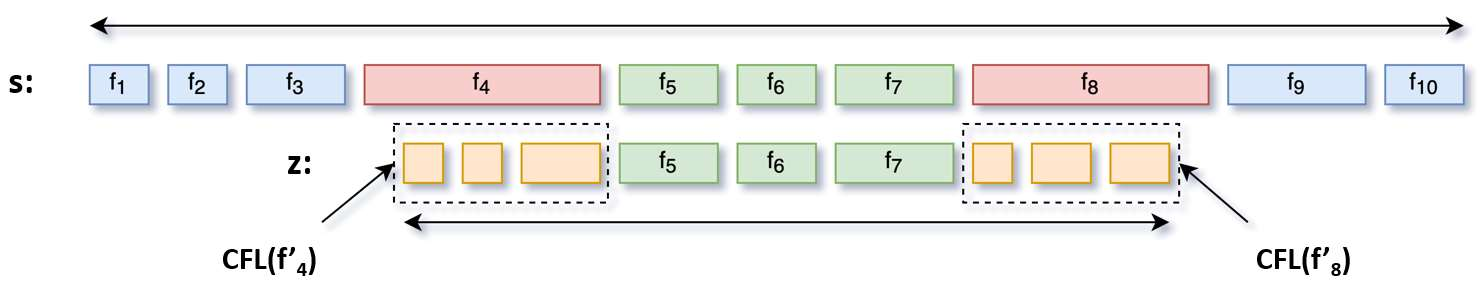
Feature embedding methods have been proposed in literature to represent sequences as numeric vectors to be used in some bioinformatics investigations, such as family classification and protein structure prediction. Recent theoretical results showed that the well-known Lyndon factorization preserves common factors in overlapping strings. Surprisingly, the fingerprint of a sequencing read, which is the sequence of lengths of consecutive factors in variants of the Lyndon factorization of the read, is effective in preserving sequence similarities, suggesting it as basis for the definition of novels representations of sequencing reads. We propose a novel feature embedding method for Next-Generation Sequencing (NGS) data using the notion of fingerprint. We provide a theoretical and experimental framework to estimate the behaviour of fingerprints and of the $k$-mers extracted from it, called $k$-fingers, as possible feature embeddings for sequencing reads. As a case study to assess the effectiveness of such embeddings, we use fingerprints to represent RNA-Seq reads and to assign them to the most likely gene from which they were originated as fragments of transcripts of the gene. We provide an implementation of the proposed method in the tool lyn2vec, which produces Lyndon-based feature embeddings of sequencing reads.
翻译:文献中提出了嵌入特性的方法,以代表一些生物信息学调查中将使用的数值矢量序列序列,如家庭分类和蛋白结构预测等。最近的理论结果显示,众所周知的林登系数化保留了重叠字符串中的常见因素。令人惊讶的是,测序读法的指纹,即朗登系数化变异数中连续因素长度的序列,有效地保存了序列相似性,建议它作为确定排序变数的新表述的基础。我们提议了用于使用指纹概念进行下基因测算(NGS)数据的新特征嵌入方法。我们提供了一个理论和实验框架,用以估计指纹和从中提取的美元-美元-米的行为,称为$-金,作为测序的可能的特征嵌入。作为评估这种嵌入效力的案例研究,我们使用指纹作为RNA-Seq读法定义的基础,并将其指定为最有可能产生基因的基因,作为基因笔录的碎片。我们提供了一个理论和实验框架,用以估计指纹和从中提取的美元-美元-美元-米的特征行为,称为美元-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-金-