Neograd: gradient descent with an adaptive learning rate

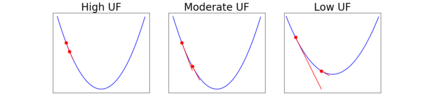
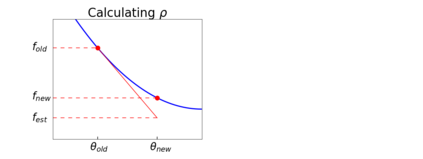
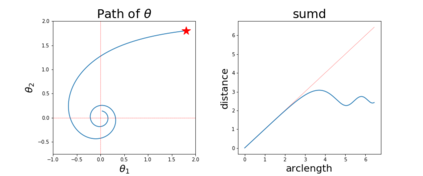
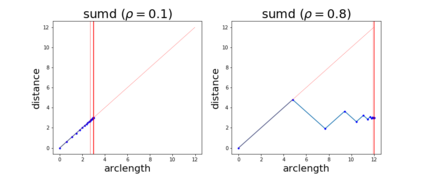
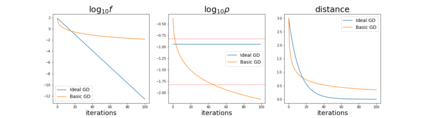
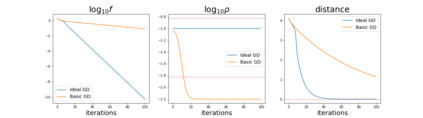
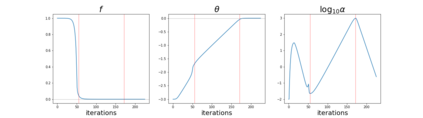
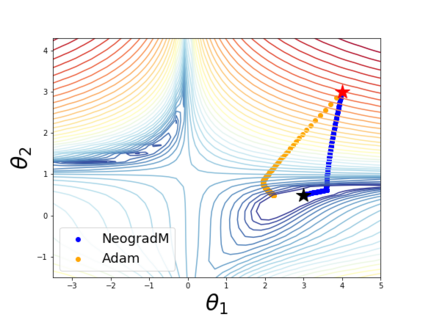
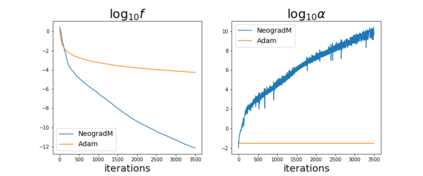
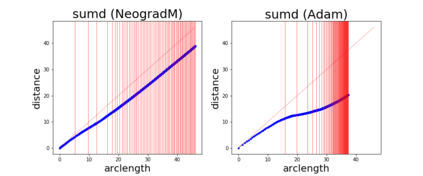
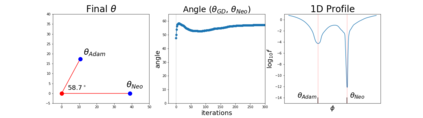
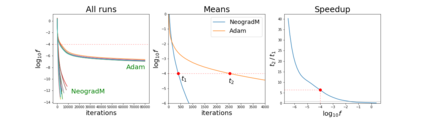
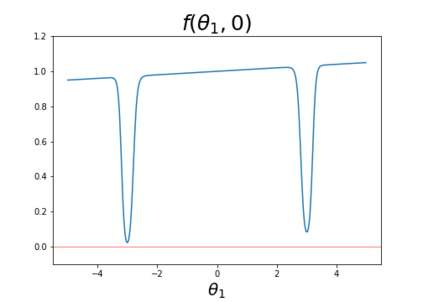
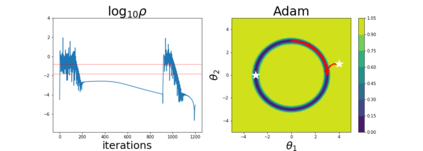
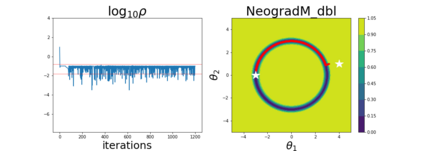
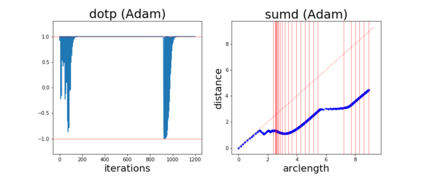
Since its inception by Cauchy in 1847, the gradient descent algorithm has been without guidance as to how to efficiently set the learning rate. This paper identifies a concept, defines metrics, and introduces algorithms to provide such guidance. The result is a family of algorithms (Neograd) based on a {\em constant $\rho$ ansatz}, where $\rho$ is a metric based on the error of the updates. This allows one to adjust the learning rate at each step, using a formulaic estimate based on $\rho$. It is now no longer necessary to do trial runs beforehand to estimate a single learning rate for an entire optimization run. The additional costs to operate this metric are trivial. One member of this family of algorithms, NeogradM, can quickly reach much lower cost function values than other first order algorithms. Comparisons are made mainly between NeogradM and Adam on an array of test functions and on a neural network model for identifying hand-written digits. The results show great performance improvements with NeogradM.