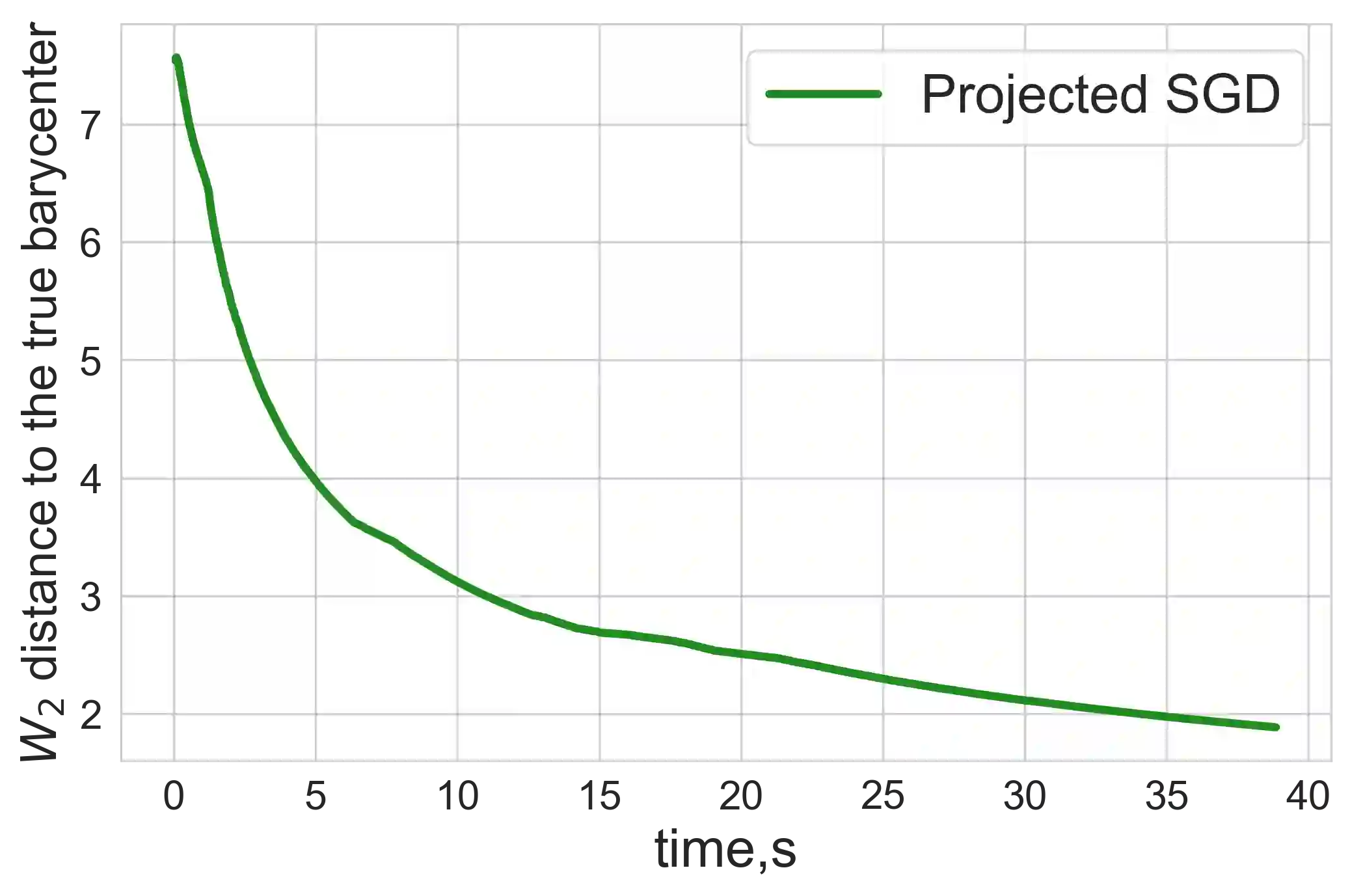
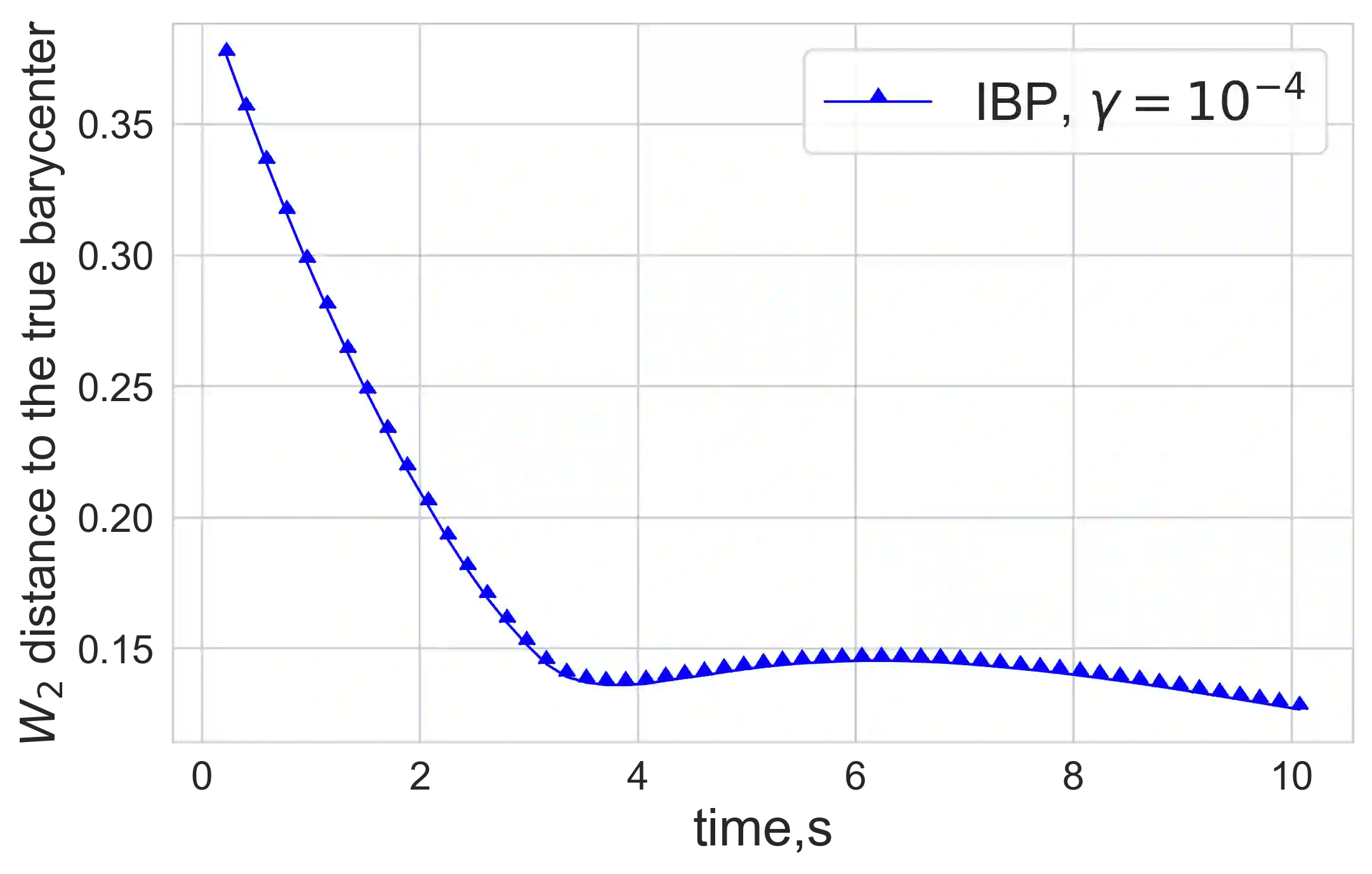
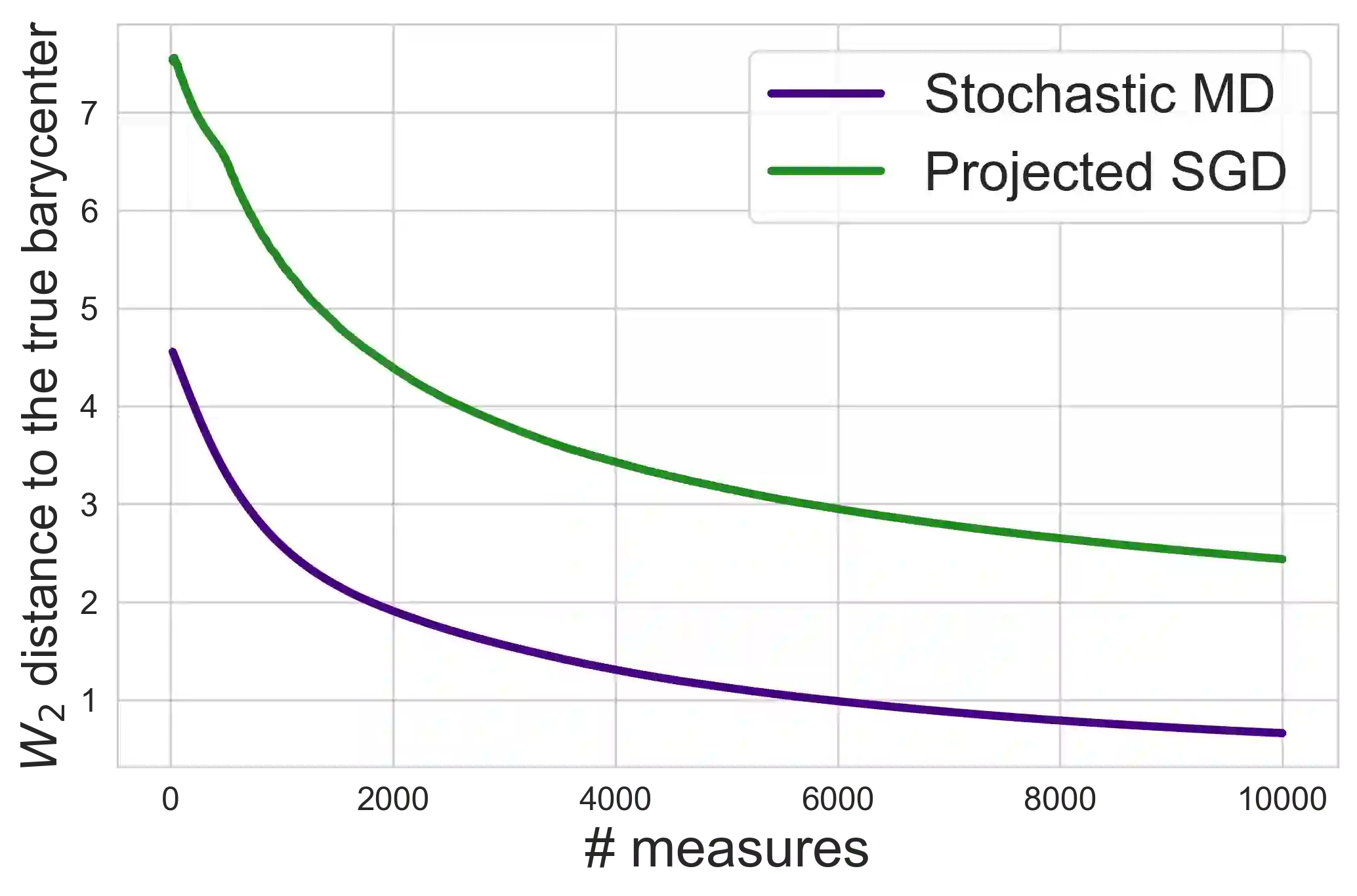
In the machine learning and optimization community, there are two main approaches for the convex risk minimization problem, namely, the Stochastic Approximation (SA) and the Sample Average Approximation (SAA). In terms of oracle complexity (required number of stochastic gradient evaluations), both approaches are considered equivalent on average (up to a logarithmic factor). The total complexity depends on the specific problem, however, starting from work \cite{nemirovski2009robust} it was generally accepted that the SA is better than the SAA. % Nevertheless, in case of large-scale problems SA may run out of memory as storing all data on one machine and organizing online access to it can be impossible without communications with other machines. SAA in contradistinction to SA allows parallel/distributed calculations. We show that for the Wasserstein barycenter problem this superiority can be inverted. We provide a detailed comparison by stating the complexity bounds for the SA and the SAA implementations calculating barycenters defined with respect to optimal transport distances and entropy-regularized optimal transport distances. As a byproduct, we also construct confidence intervals for the barycenter defined with respect to entropy-regularized optimal transport distances in the $\ell_2$-norm. The preliminary results are derived for a general convex optimization problem given by the expectation in order to have other applications besides the Wasserstein barycenter problem.
翻译:在机器学习和优化过程中,对于最小化风险问题,有两种主要的方法,即:斯托切吸附(SA)和样本平均吸附(SAA),这主要有两种办法。在分解复杂程度(要求的随机梯度评价数量)方面,这两种办法都被视为平均相等(直至对数系数)。然而,总复杂程度取决于具体的问题,但从工作开始,人们普遍认为SA比SAA要好。 然而,如果出现大规模问题,SA可能失去记忆,因为将所有数据储存在一台机器上,组织在线访问它可能没有与其他机器的通信。SA与SA的反对异度计算允许平行/分布计算。我们表明,对于瓦瑟斯坦的中点问题,这种优越性可以被反省。我们通过说明SA的复杂程度和SAA的执行过程比SA要好。 然而,如果大范围的问题是存储在一个机器上的所有数据存储所有数据,而没有与其他机器进行在线访问,那么,SAAA可能无法使用它。