Convergent autoencoder approximation of low bending and low distortion manifold embeddings

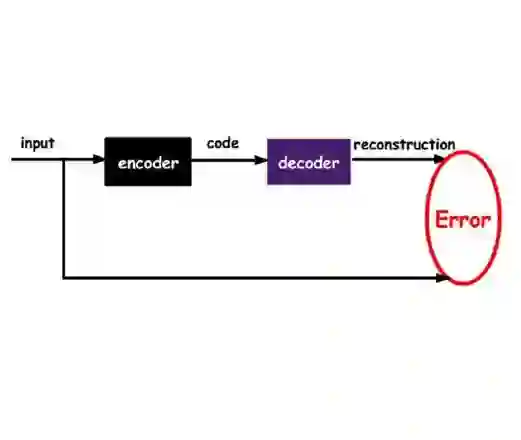
Autoencoders, which consist of an encoder and a decoder, are widely used in machine learning for dimension reduction of high-dimensional data. The encoder embeds the input data manifold into a lower-dimensional latent space, while the decoder represents the inverse map, providing a parametrization of the data manifold by the manifold in latent space. A good regularity and structure of the embedded manifold may substantially simplify further data processing tasks such as cluster analysis or data interpolation. We propose and analyze a novel regularization for learning the encoder component of an autoencoder: a loss functional that prefers isometric, extrinsically flat embeddings and allows to train the encoder on its own. To perform the training it is assumed that for pairs of nearby points on the input manifold their local Riemannian distance and their local Riemannian average can be evaluated. The loss functional is computed via Monte Carlo integration with different sampling strategies for pairs of points on the input manifold. Our main theorem identifies a geometric loss functional of the embedding map as the $\Gamma$-limit of the sampling-dependent loss functionals. Numerical tests, using image data that encodes different explicitly given data manifolds, show that smooth manifold embeddings into latent space are obtained. Due to the promotion of extrinsic flatness, these embeddings are regular enough such that interpolation between not too distant points on the manifold is well approximated by linear interpolation in latent space as one possible postprocessing.