A parallel implementation of a diagonalization-based parallel-in-time integrator

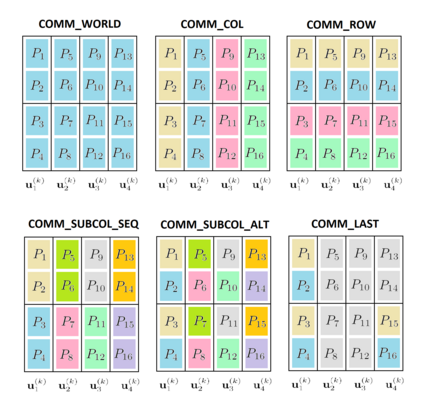
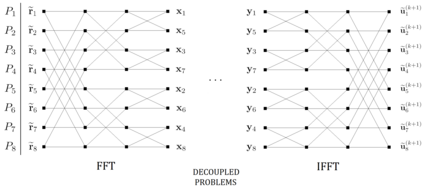
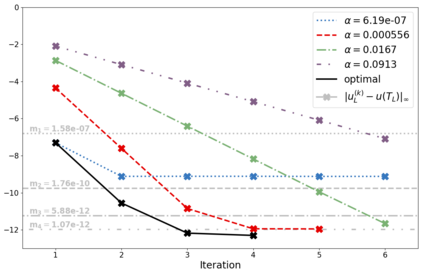
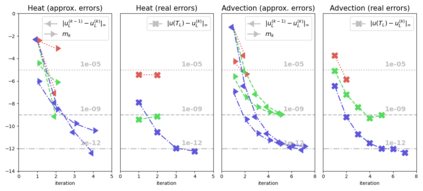
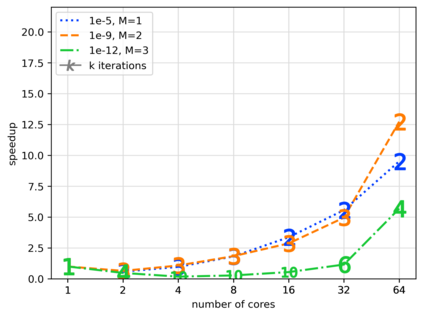
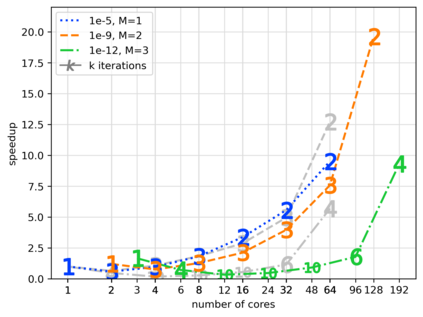
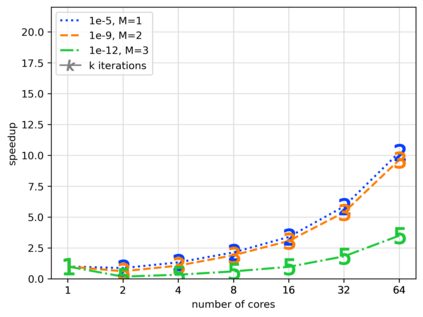
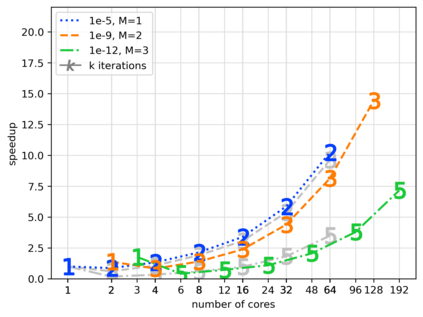
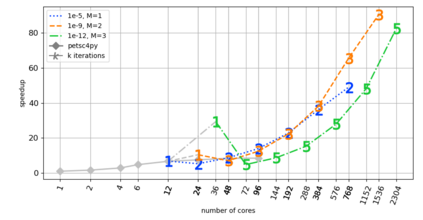
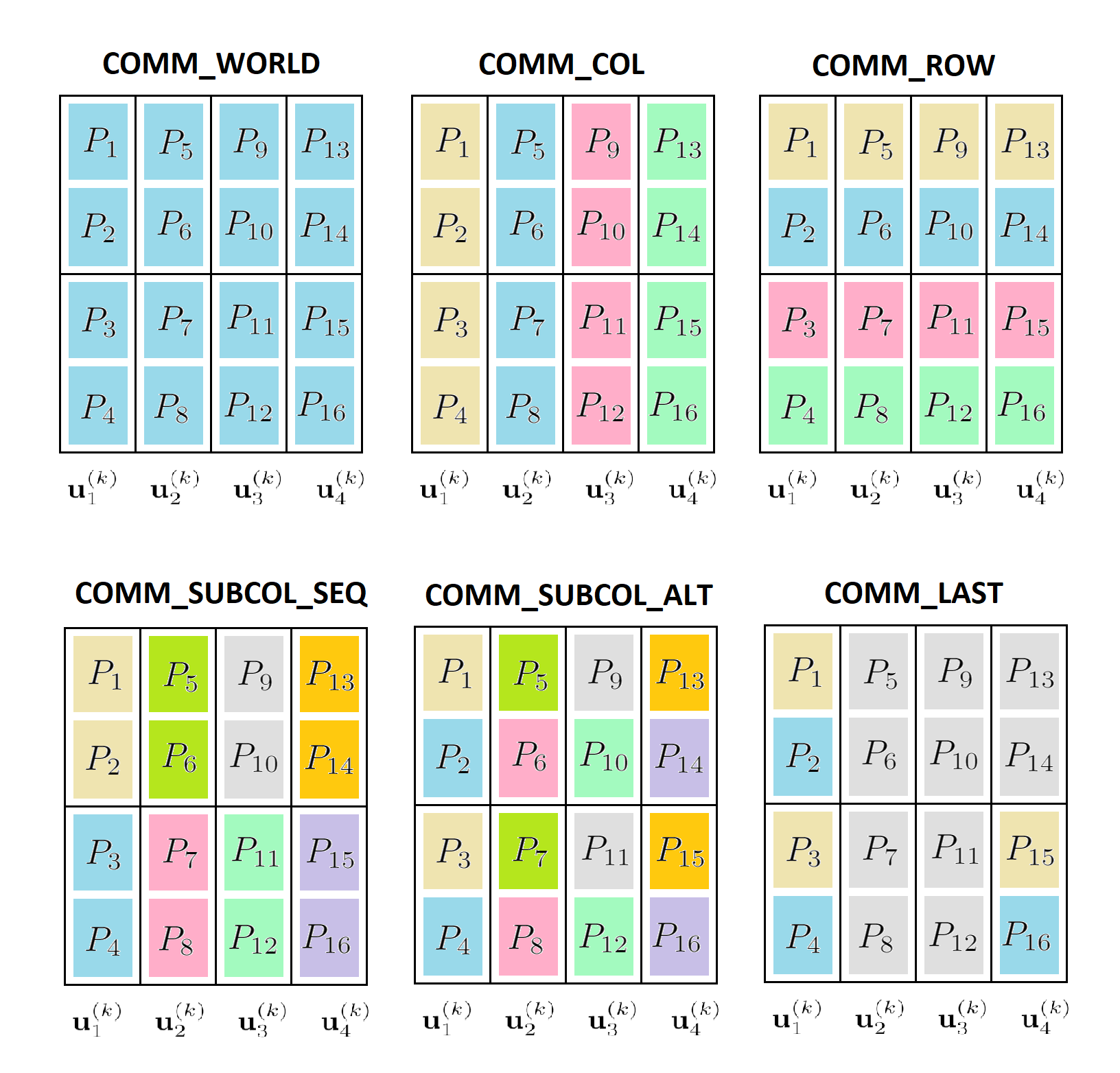
We present and analyze a parallel implementation of a parallel-in-time method based on $\alpha$-circulant preconditioned Richardson iterations. While there are a lot of papers exploring this new class of single-level, time-parallel integrators from many perspectives, performance results of actual parallel runs are still missing. This leaves a critical gap, because the efficiency and applicability heavily rely on the actual parallel performance, with only limited guidance from theoretical considerations. Also, many challenges like selecting good parameters, finding suitable communication strategies, and performing a fair comparison to sequential time-stepping methods can be easily missed. In this paper, we first extend the original idea by using a collocation method of arbitrary order, which adds another level of parallelization in time. We derive an adaptive strategy to select a new $\alpha$-circulant preconditioner for each iteration during runtime for balancing convergence rates, round-off errors and inexactness in the individual time-steps. After addressing these more theoretical challenges, we present an open-source space- and doubly-time-parallel implementation and evaluate its performance for two different test problems.