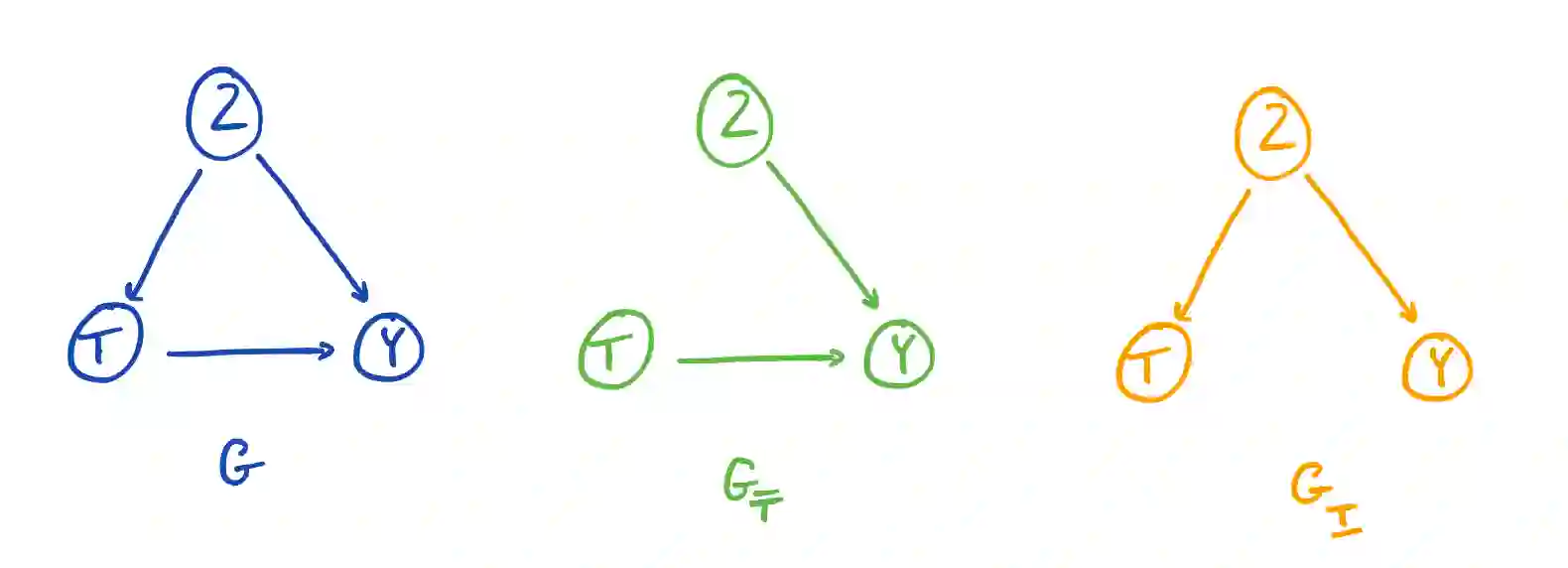
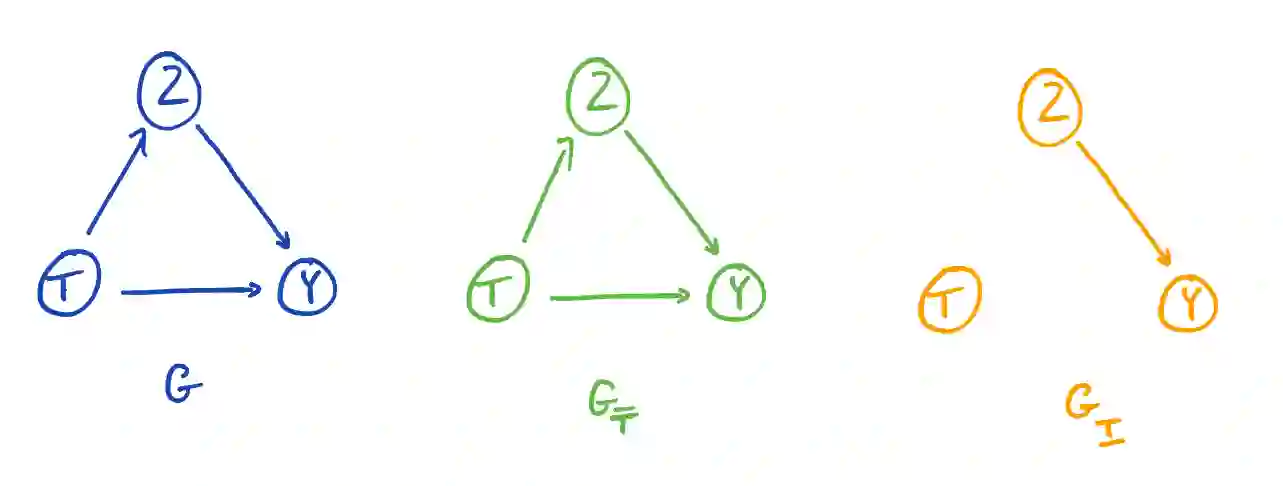
The concept of causality has a controversial history. The question of whether it is possible to represent and address causal problems with probability theory, or if fundamentally new mathematics such as the do calculus is required has been hotly debated, e.g. Pearl (2001) states "the building blocks of our scientific and everyday knowledge are elementary facts such as "mud does not cause rain" and "symptoms do not cause disease" and those facts, strangely enough, cannot be expressed in the vocabulary of probability calculus". This has lead to a dichotomy between advocates of causal graphical modeling and the do calculus, and researchers applying Bayesian methods. In this paper we demonstrate that, while it is critical to explicitly model our assumptions on the impact of intervening in a system, provided we do so, estimating causal effects can be done entirely within the standard Bayesian paradigm. The invariance assumptions underlying causal graphical models can be encoded in ordinary Probabilistic graphical models, allowing causal estimation with Bayesian statistics, equivalent to the do calculus. Elucidating the connections between these approaches is a key step toward enabling the insights provided by each to be combined to solve real problems.
翻译:因果关系的概念有争议的历史。 能否用概率理论来代表并解决因果关系问题,或者是否需要诸如“ 微积分” 等根本的新数学,这个问题已经引起了激烈的辩论,例如Pearl (2001年) 指出, “ 我们科学和日常知识的构件是基本事实, 如“ 哺乳不会造成降雨” 和“ 症状不会造成疾病 ”, 而这些事实,奇怪的是无法用概率微积分的词汇来表达。 这导致因果图形模型和多微积分的倡导者与运用巴耶斯方法的研究人员之间的分化。 在本文中,我们表明,尽管明确模拟我们对干预系统的影响的假设至关重要,但只要我们这样做,估计因果关系可以完全在标准巴伊斯范式范围内进行。 因果关系图形模型的不一致性假设可以在普通的“ 概率图形模型” 中进行编码, 允许用贝亚斯统计的因果关系估算, 等同于“ 计算” 。 判断这些方法之间的联系是使每个问题都能被综合到真正解决问题的关键一步。