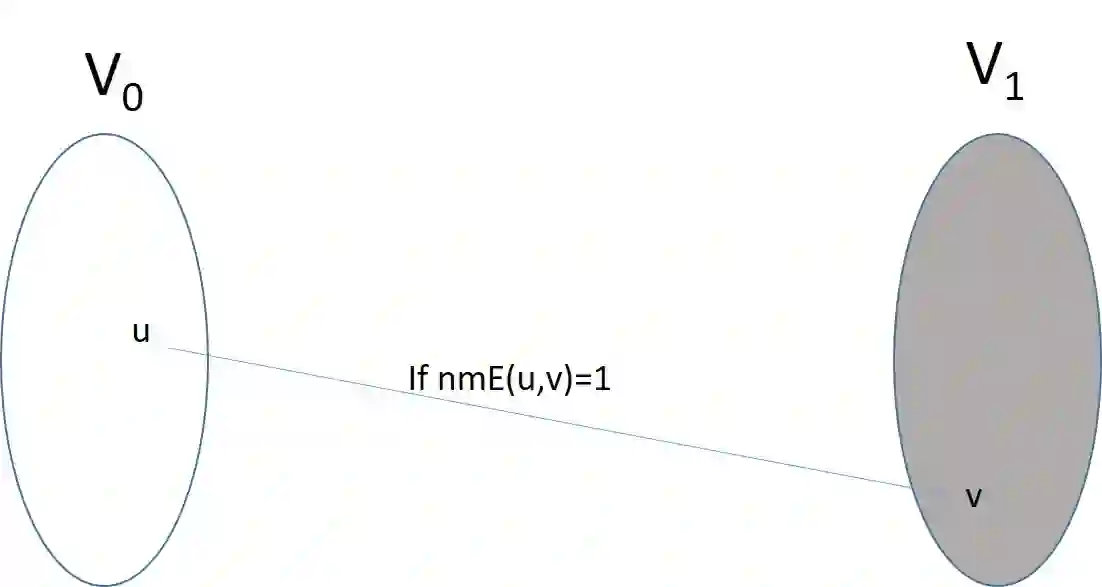
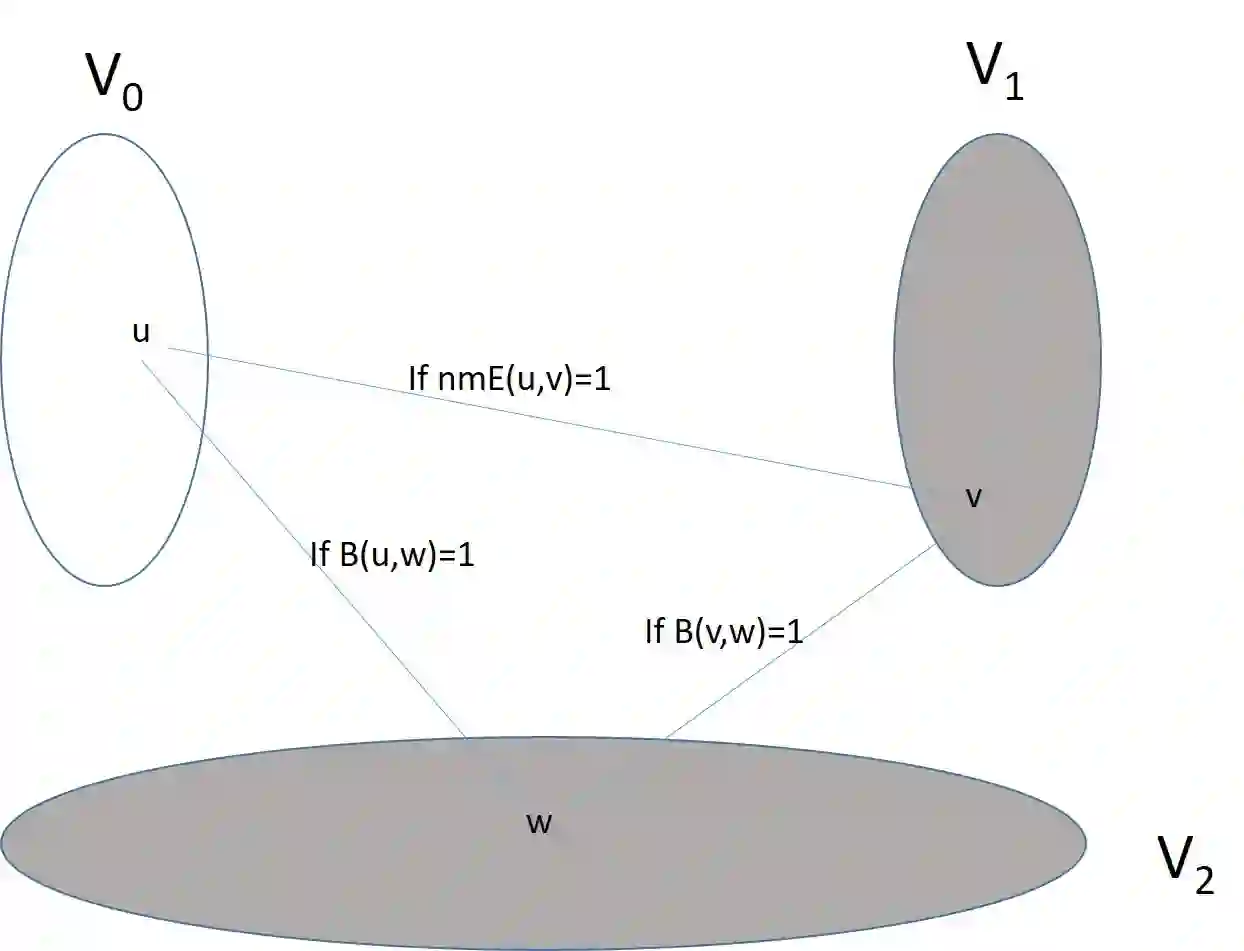
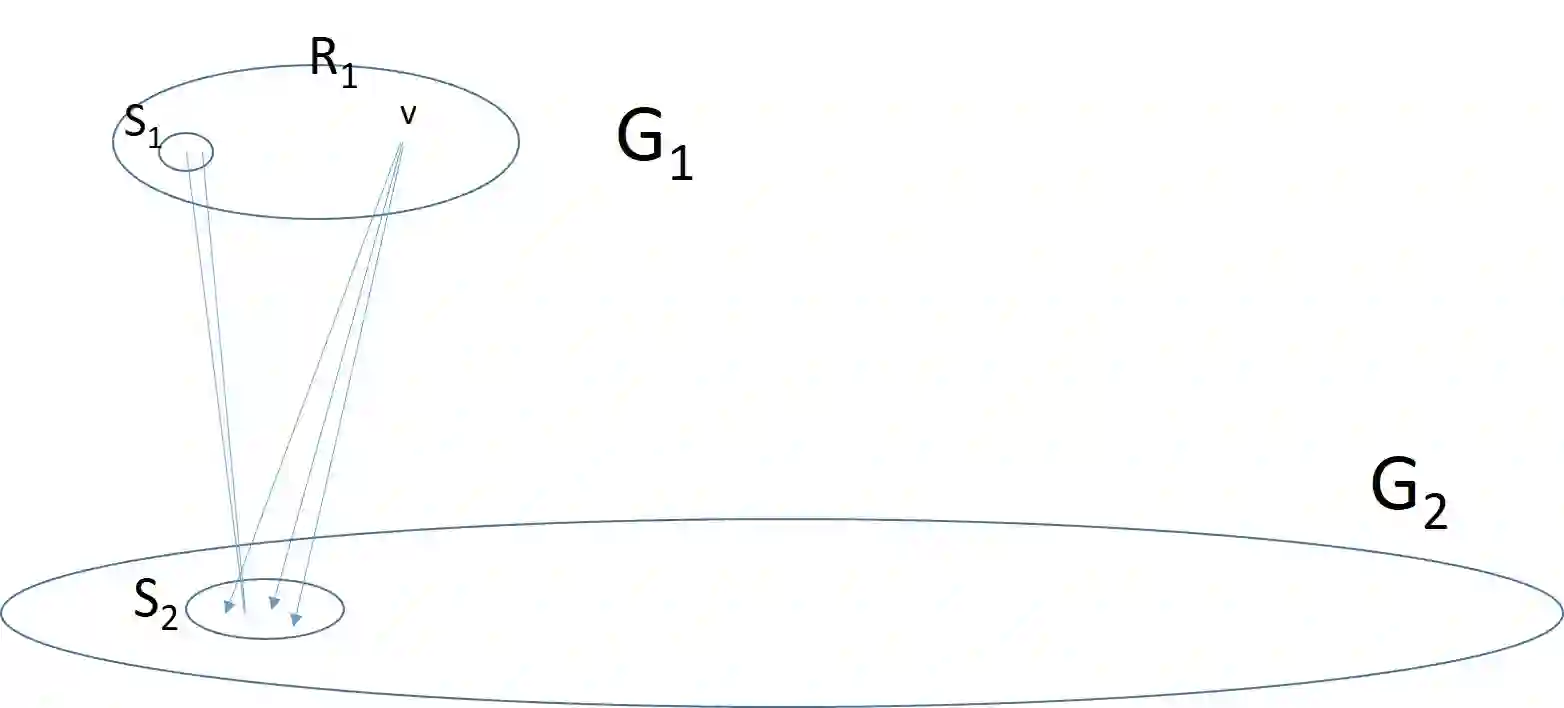
A graph $G$ is called self-ordered (a.k.a asymmetric) if the identity permutation is its only automorphism. Equivalently, there is a unique isomorphism from $G$ to any graph that is isomorphic to $G$. We say that $G=(V,E)$ is robustly self-ordered if the size of the symmetric difference between $E$ and the edge-set of the graph obtained by permuting $V$ using any permutation $\pi:V\to V$ is proportional to the number of non-fixed-points of $\pi$. In this work, we initiate the study of the structure, construction and utility of robustly self-ordered graphs. We show that robustly self-ordered bounded-degree graphs exist (in abundance), and that they can be constructed efficiently, in a strong sense. Specifically, given the index of a vertex in such a graph, it is possible to find all its neighbors in polynomial-time (i.e., in time that is poly-logarithmic in the size of the graph). We also consider graphs of unbounded degree, seeking correspondingly unbounded robustness parameters. We again demonstrate that such graphs (of linear degree) exist (in abundance), and that they can be constructed efficiently, in a strong sense. This turns out to require very different tools. Specifically, we show that the construction of such graphs reduces to the construction of non-malleable two-source extractors (with very weak parameters but with some additional natural features). We demonstrate that robustly self-ordered bounded-degree graphs are useful towards obtaining lower bounds on the query complexity of testing graph properties both in the bounded-degree and the dense graph models. One of the results that we obtain, via such a reduction, is a subexponential separation between the query complexities of testing and tolerant testing of graph properties in the bounded-degree graph model.
翻译:图形 $G$ 被称为自序( a.k. a mal- g$) 。 如果身份变色是唯一的自动变色。 等量地, 则身份变色是一种独特的异形, 从$G$到任何非正态至美元。 我们说, $G=( V, E) 美元是一个强烈的自序, 如果对称美元与以任何变色法 $V美元获得的图表的边缘值的大小是自序的( a.k. k. a 不对称): 如果身份变色是唯一的自动变色。 如果身份变色( a.k.k.a.al-to V) 与非固定点的变色调值成比例成正比。 在此工作中, 我们开始研究强度的自序变色图的结构、构造变色变色度和变色变色的变色度。 我们的变色变色变色的变色变色度, 我们的变色变色的变色的变色度, 我们的变色变色的变色的变色的变色的变色的变色的变色, 我们的变色变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色的变色。