Kernel Aggregated Fast Multipole Method: Efficient summation of Laplace and Stokes kernel functions

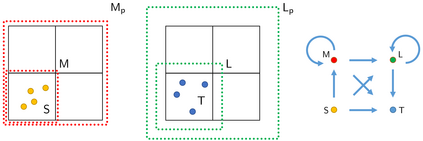
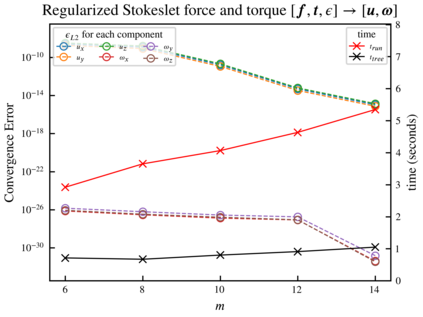
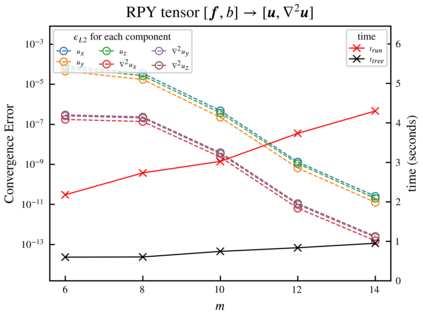
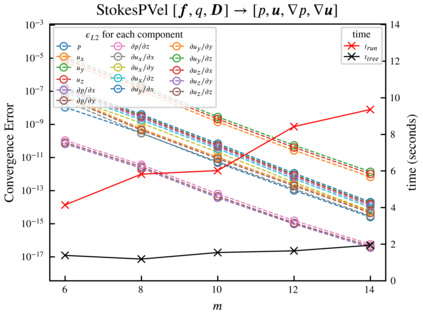
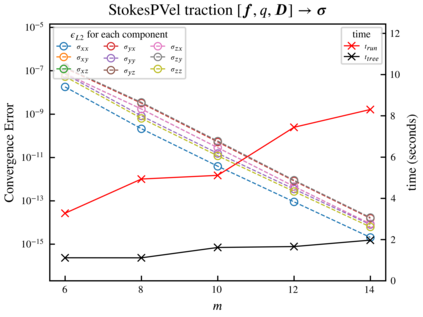
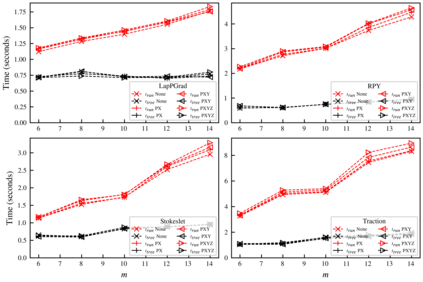
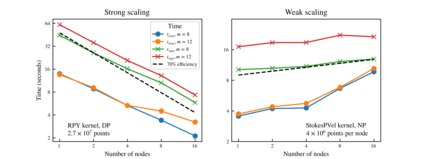
Many different simulation methods for Stokes flow problems involve a common computationally intense task -- the summation of a kernel function over $O(N^2)$ pairs of points. One popular technique is the Kernel Independent Fast Multipole Method (KIFMM), which constructs a spatial adaptive octree for all points and places a small number of equivalent multipole and local equivalent points around each octree box, and completes the kernel sum with $O(N)$ cost, using these equivalent points. Simpler kernels can be used between these equivalent points to improve the efficiency of KIFMM. Here we present further extensions and applications to this idea, to enable efficient summations and flexible boundary conditions for various kernels. We call our method the Kernel Aggregated Fast Multipole Method (KAFMM), because it uses different kernel functions at different stages of octree traversal. We have implemented our method as an open-source software library STKFMM based on the high performance library PVFMM, with support for Laplace kernels, the Stokeslet, regularized Stokeslet, Rotne-Prager-Yamakawa (RPY) tensor, and the Stokes double-layer and traction operators. Open and periodic boundary conditions are supported for all kernels, and the no-slip wall boundary condition is supported for the Stokeslet and RPY tensor. The package is designed to be ready-to-use as well as being readily extensible to additional kernels.