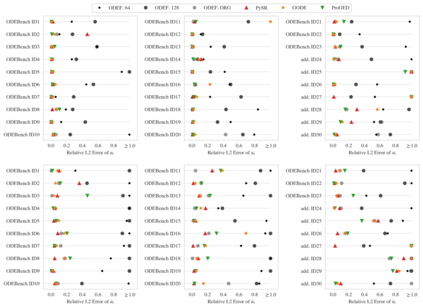
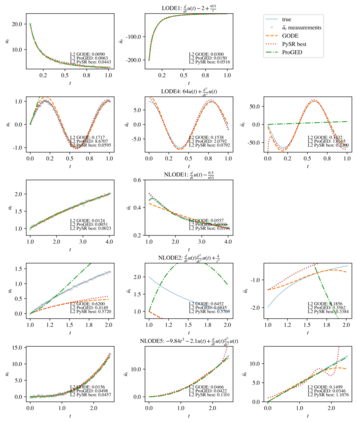
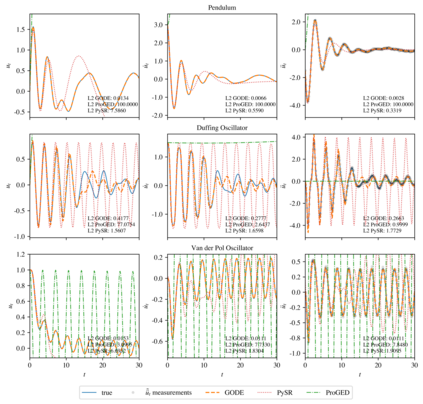
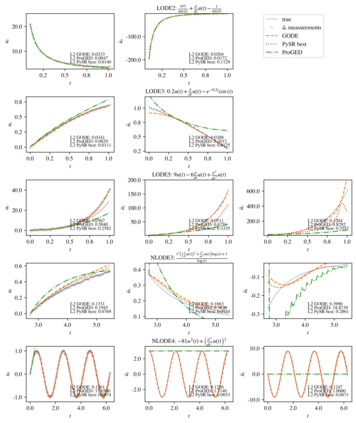
The understanding and modeling of complex physical phenomena through dynamical systems has historically driven scientific progress, as it provides the tools for predicting the behavior of different systems under diverse conditions through time. The discovery of dynamical systems has been indispensable in engineering, as it allows for the analysis and prediction of complex behaviors for computational modeling, diagnostics, prognostics, and control of engineered systems. Joining recent efforts that harness the power of symbolic regression in this domain, we propose a novel framework for the end-to-end discovery of ordinary differential equations (ODEs), termed Grammar-based ODE Discovery Engine (GODE). The proposed methodology combines formal grammars with dimensionality reduction and stochastic search for efficiently navigating high-dimensional combinatorial spaces. Grammars allow us to seed domain knowledge and structure for both constraining, as well as, exploring the space of candidate expressions. GODE proves to be more sample- and parameter-efficient than state-of-the-art transformer-based models and to discover more accurate and parsimonious ODE expressions than both genetic programming- and other grammar-based methods for more complex inference tasks, such as the discovery of structural dynamics. Thus, we introduce a tool that could play a catalytic role in dynamics discovery tasks, including modeling, system identification, and monitoring tasks.
翻译:暂无翻译