Analysis of a finite-volume scheme for a single-species biofilm model

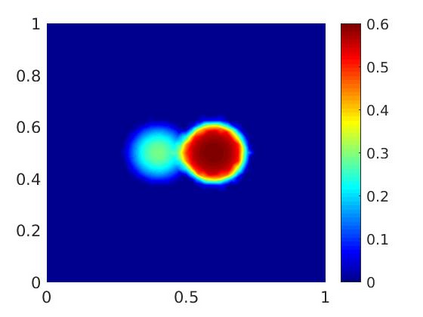
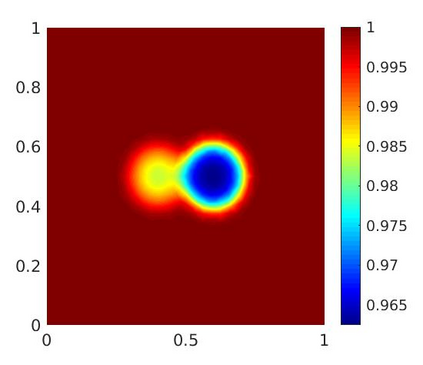
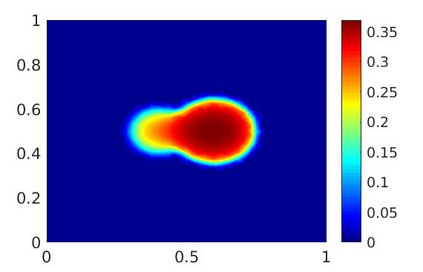
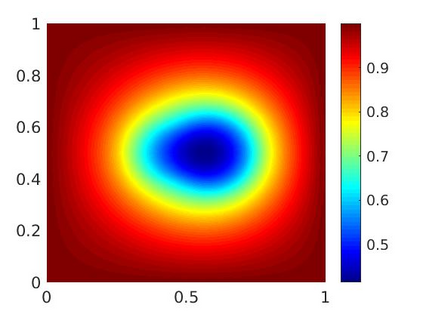
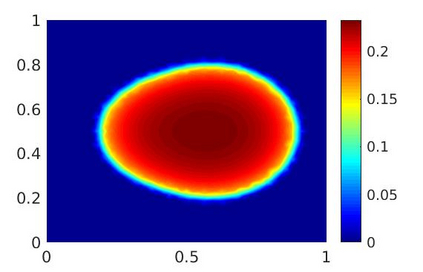
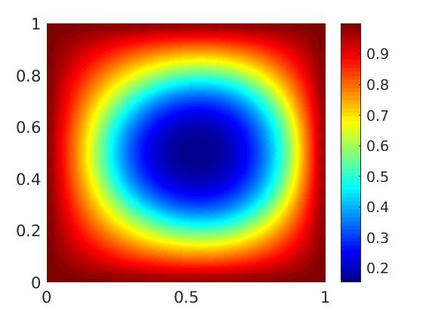
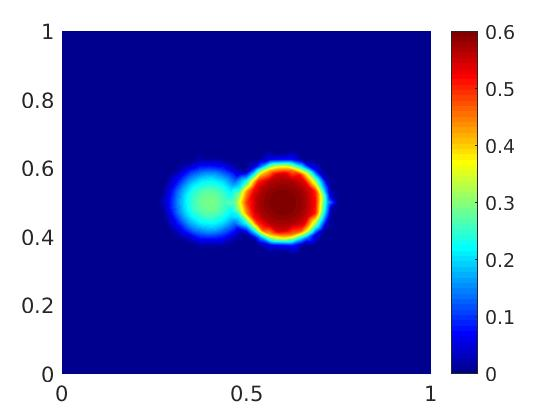
An implicit Euler finite-volume scheme for a parabolic reaction-diffusion system modeling biofilm growth is analyzed and implemented. The system consists of a degenerate-singular diffusion equation for the biomass fraction, which is coupled to a diffusion equation for the nutrient concentration, and it is solved in a bounded domain with Dirichlet boundary conditions. By transforming the biomass fraction to an entropy-type variable, it is shown that the numerical scheme preserves the lower and upper bounds of the biomass fraction. The existence and uniqueness of a discrete solution and the convergence of the scheme are proved. Numerical experiments in one and two space dimensions illustrate, respectively, the rate of convergence in space of our scheme and the temporal evolution of the biomass fraction and the nutrient concentration.