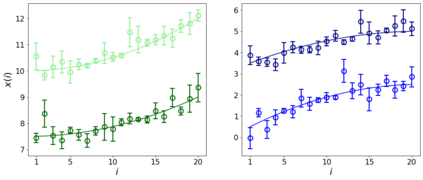
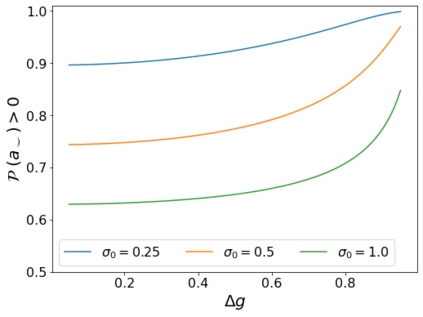
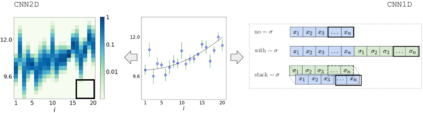
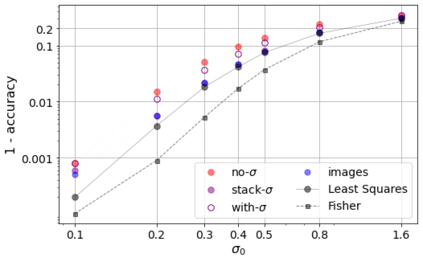
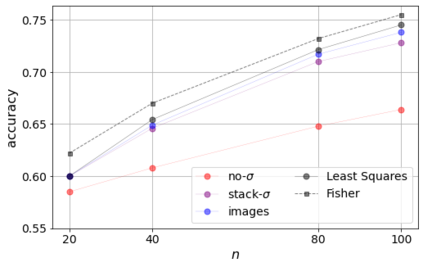
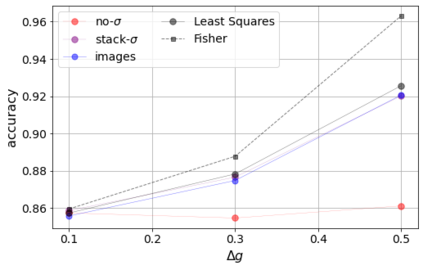
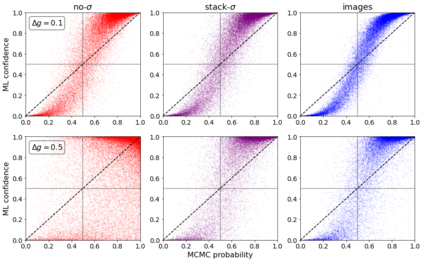
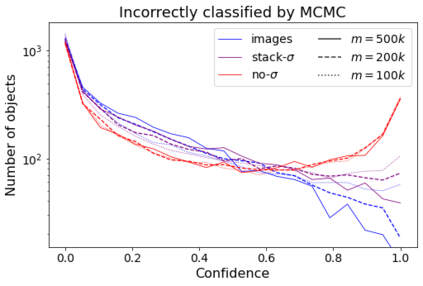
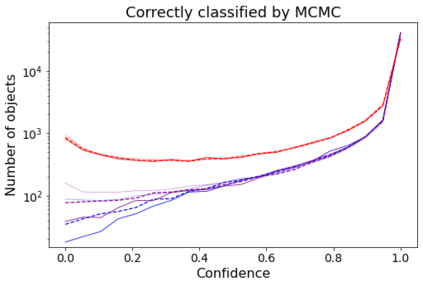
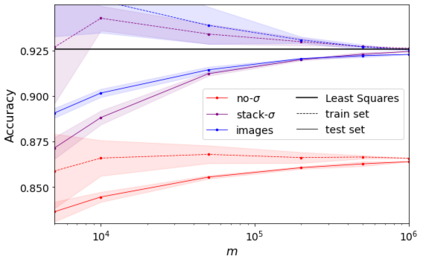
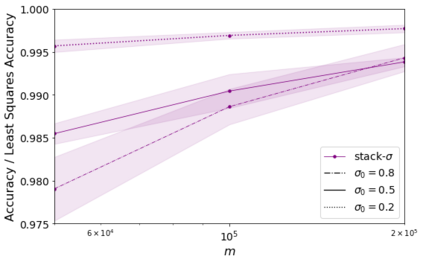
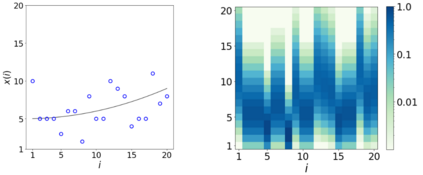
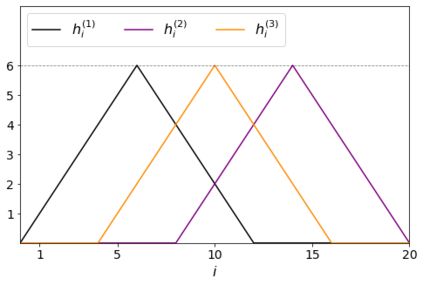
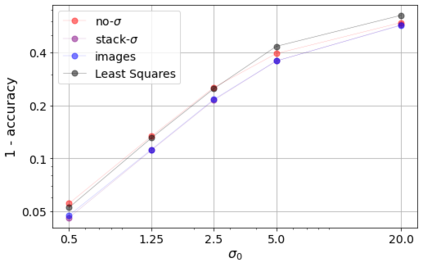
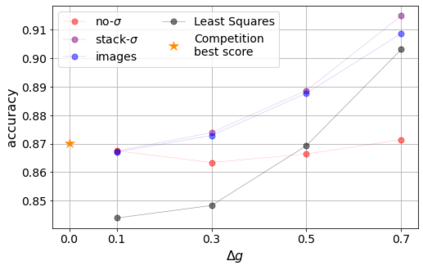
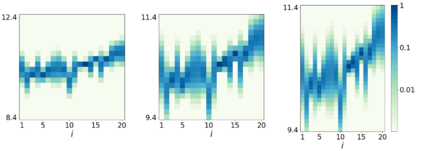
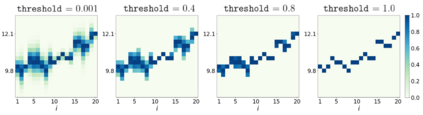
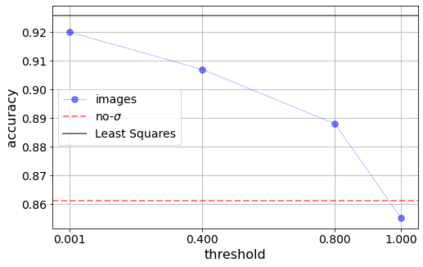
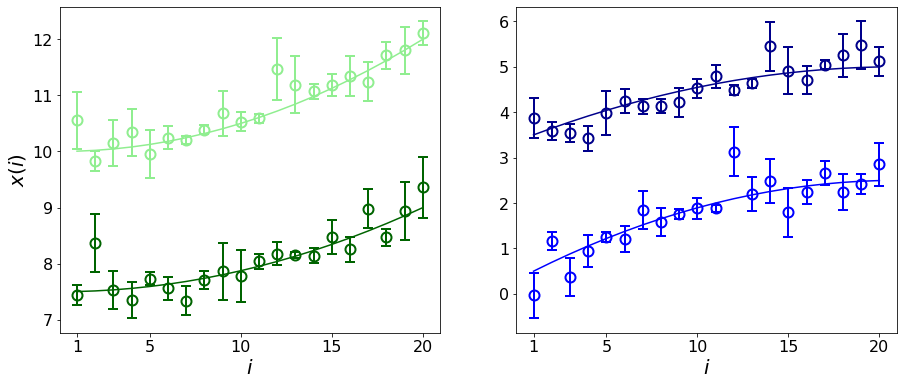
Errors in measurements are key to weighting the value of data, but are often neglected in Machine Learning (ML). We show how Convolutional Neural Networks (CNNs) are able to learn about the context and patterns of signal and noise, leading to improvements in the performance of classification methods. We construct a model whereby two classes of objects follow an underlying Gaussian distribution, and where the features (the input data) have varying, but known, levels of noise. This model mimics the nature of scientific data sets, where the noises arise as realizations of some random processes whose underlying distributions are known. The classification of these objects can then be performed using standard statistical techniques (e.g., least-squares minimization or Markov-Chain Monte Carlo), as well as ML techniques. This allows us to take advantage of a maximum likelihood approach to object classification, and to measure the amount by which the ML methods are incorporating the information in the input data uncertainties. We show that, when each data point is subject to different levels of noise (i.e., noises with different distribution functions), that information can be learned by the CNNs, raising the ML performance to at least the same level of the least-squares method -- and sometimes even surpassing it. Furthermore, we show that, with varying noise levels, the confidence of the ML classifiers serves as a proxy for the underlying cumulative distribution function, but only if the information about specific input data uncertainties is provided to the CNNs.
翻译:测量错误是衡量数据价值的关键,但在机器学习(ML)中常常被忽略。 我们展示了进化神经网络(CNNs)如何能够了解信号和噪音的背景和模式,从而改进了分类方法的性能。 我们构建了一个模型,让两类对象遵循高斯分布法,而其中的特性(输入数据)具有不同但已知的噪音水平。这个模型模仿了科学数据集的性质,其中的噪音是随着某些随机过程的实现而出现的,而该过程的根基分布为已知。然后,这些对象的分类可以使用标准的统计技术(例如,最小最小最小最小值或Markov-Chain Monte Carlo)以及ML技术来进行,这使我们能够利用最大可能性的方法来进行物体分类,并测量ML方法将信息纳入输入数据不确定性的程度。 我们显示,如果每个数据点都受到不同程度的噪音(例如,具有不同分布功能的噪音)的影响,那么这些对象的分类可以使用标准的统计技术(例如,最小最小最小的平方或最低端值 MCarlota ) 技术进行。 这让我们能够以最小的超度的方式显示其底值数据。