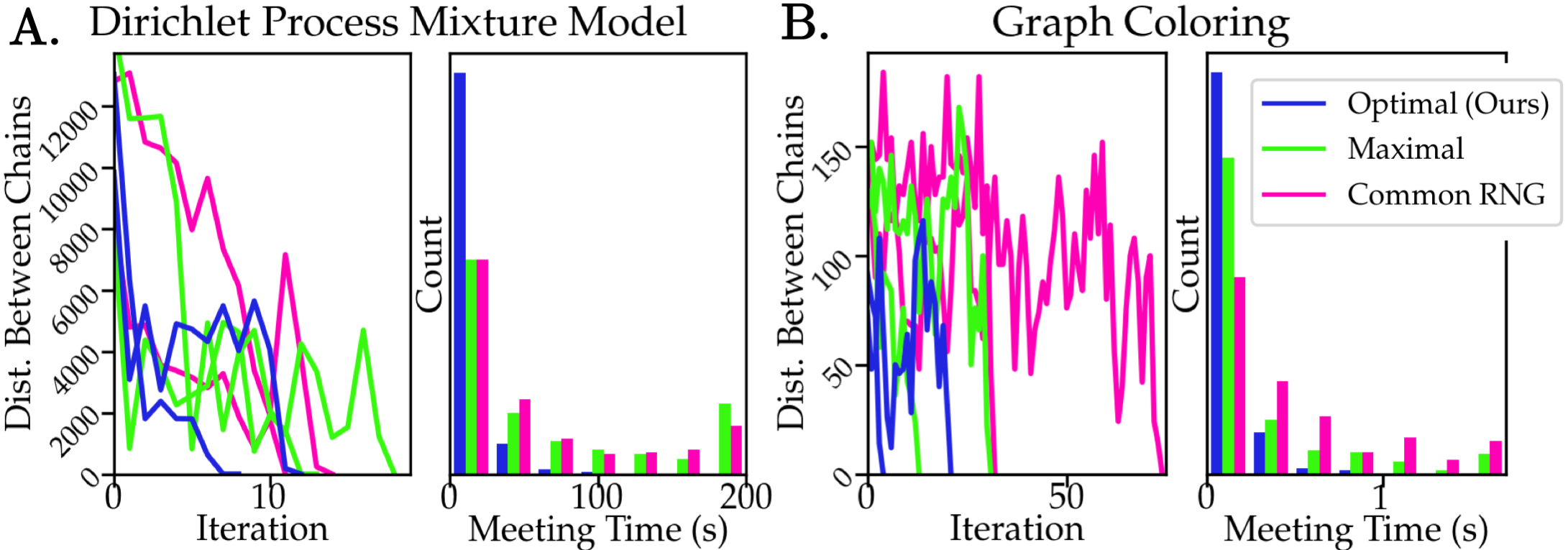
Computational couplings of Markov chains provide a practical route to unbiased Monte Carlo estimation that can utilize parallel computation. However, these approaches depend crucially on chains meeting after a small number of transitions. For models that assign data into groups, e.g. mixture models, the obvious approaches to couple Gibbs samplers fail to meet quickly. This failure owes to the so-called "label-switching" problem; semantically equivalent relabelings of the groups contribute well-separated posterior modes that impede fast mixing and cause large meeting times. We here demonstrate how to avoid label switching by considering chains as exploring the space of partitions rather than labelings. Using a metric on this space, we employ an optimal transport coupling of the Gibbs conditionals. This coupling outperforms alternative couplings that rely on labelings and, on a real dataset, provides estimates more precise than usual ergodic averages in the limited time regime. Code is available at github.com/tinnguyen96/coupling-Gibbs-partition.
翻译:Markov 链条的计算连接提供了一条实用的路径,可以用来进行公正的蒙特卡洛估计,从而利用平行的计算。然而,这些方法关键地取决于在少数转换之后的链子会议。对于将数据分解成组的模型,例如混合模型,Gibbs取样器的明显方法无法迅速相遇。由于所谓的“标签开动”问题,这些组群的基因等同的重新标签造成了良好的分离远地点模式,妨碍快速混合并造成大量会议时间。我们在这里展示了如何避免标签转换,将链子视为探索分区空间,而不是标签。我们在这个空间使用一个指标,我们采用了一种最佳的将Gibs条件连接的连接方式。这种组合比替代的组合更精确,它依赖标签,并且根据真实的数据集,提供比有限时间制度中通常的异位平均数更精确的估计数。代码可在 Ginthubub.com/tinguyen96/cupling-Gibbbs-parttion中查阅。