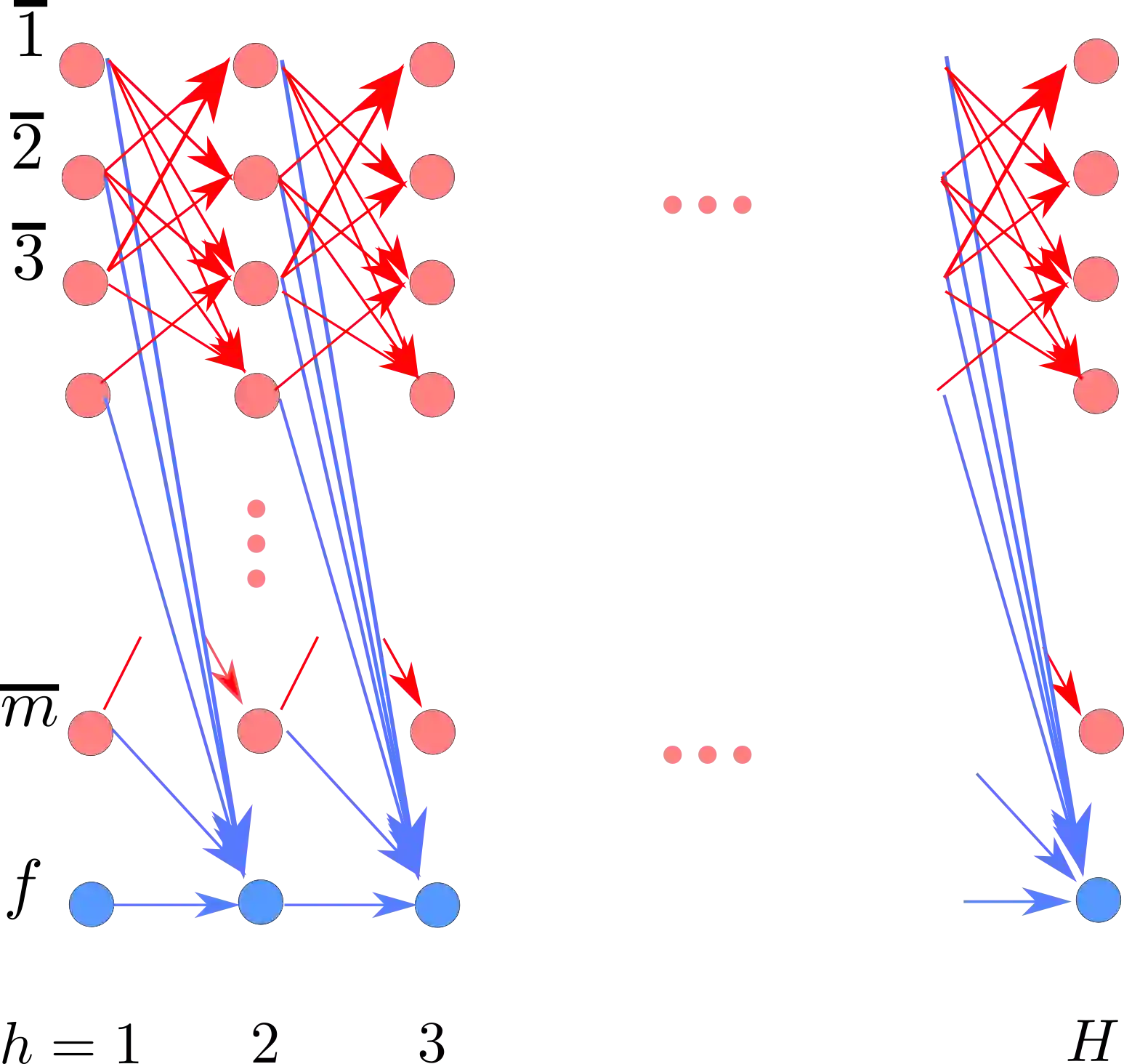
A fundamental question in the theory of reinforcement learning is: suppose the optimal $Q$-function lies in the linear span of a given $d$ dimensional feature mapping, is sample-efficient reinforcement learning (RL) possible? The recent and remarkable result of Weisz et al. (2020) resolved this question in the negative, providing an exponential (in $d$) sample size lower bound, which holds even if the agent has access to a generative model of the environment. One may hope that this information theoretic barrier for RL can be circumvented by further supposing an even more favorable assumption: there exists a \emph{constant suboptimality gap} between the optimal $Q$-value of the best action and that of the second-best action (for all states). The hope is that having a large suboptimality gap would permit easier identification of optimal actions themselves, thus making the problem tractable; indeed, provided the agent has access to a generative model, sample-efficient RL is in fact possible with the addition of this more favorable assumption. This work focuses on this question in the standard online reinforcement learning setting, where our main result resolves this question in the negative: our hardness result shows that an exponential sample complexity lower bound still holds even if a constant suboptimality gap is assumed in addition to having a linearly realizable optimal $Q$-function. Perhaps surprisingly, this implies an exponential separation between the online RL setting and the generative model setting. Complementing our negative hardness result, we give two positive results showing that provably sample-efficient RL is possible either under an additional low-variance assumption or under a novel hypercontractivity assumption (both implicitly place stronger conditions on the underlying dynamics model).
翻译:强化学习理论的一个根本问题是:假设最佳的 $Q 功能在于给定的 $美元 维维特特征绘图的线性跨度中的最佳 $ Q 功能在于给定的 美元 维兹 et al. (2020年) 的最近和显著的结果解决了这个问题的负数,提供了指数(以美元计) 样本大小的较低约束,即使该代理商能够利用环境的基因化模型,也保持了这一限制。人们可能会希望,如果该代理商能够通过进一步的更有利的假设来绕过RL的这一信息性障碍:在最佳行动和第二最佳行动(对所有州)的最佳 之间,存在着一个 QQ(RL 2020 ) 的样本效率强(RL ) 的精度强化学习(RL )? 这一问题的精确度在标准 基底比值的精确度假设中表现了一种硬性结果, 也就是在最精确的精确的假设下, 直线性结果显示一个硬性结果, 在最精确的精确的假设下, 在最精确的假设之下,一个硬性结果显示一个硬性结果的精确的精确的精确的假设 。