Bandit Learning for Dynamic Colonel Blotto Game with a Budget Constraint

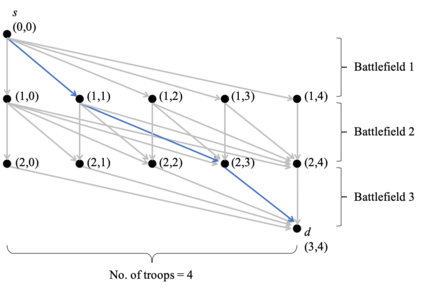
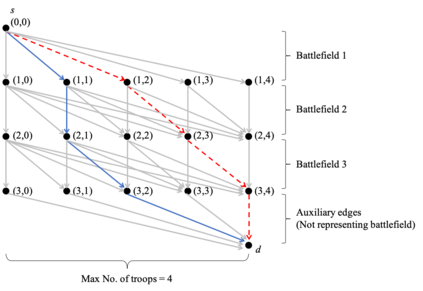
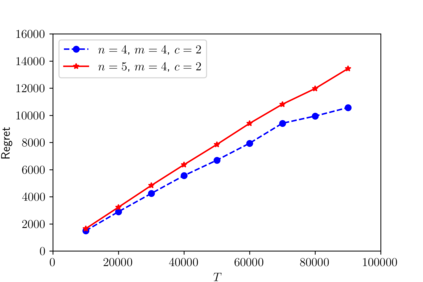
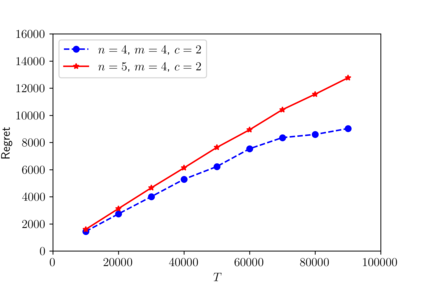
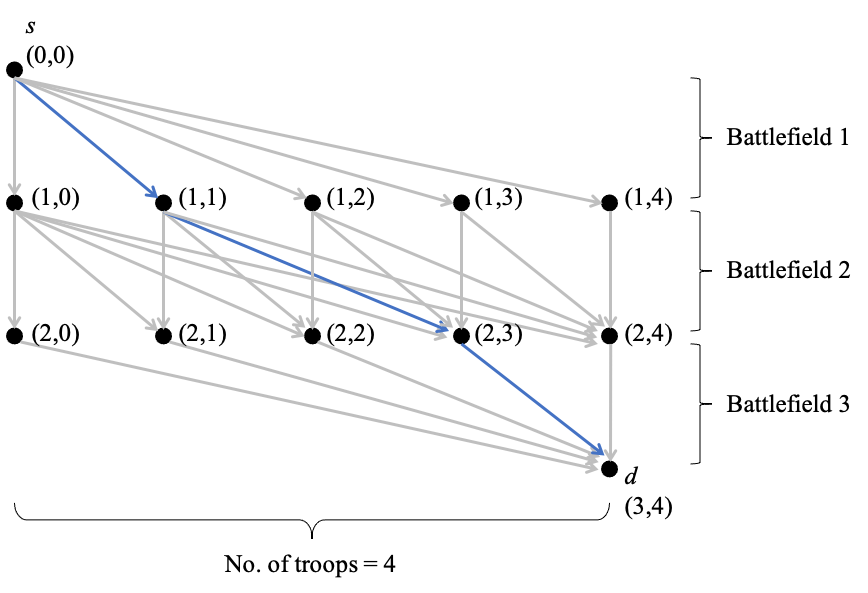
We consider a dynamic Colonel Blotto game (CBG) in which one of the players is the learner and has limited troops (budget) to allocate over a finite time horizon. At each stage, the learner strategically determines the budget distribution among the battlefields based on past observations. The other player is the adversary, who chooses its budget allocation strategies randomly from some fixed unknown distribution. The learner's objective is to minimize its regret, which is the difference between the payoff of the best mixed strategy and the realized payoff by following a learning algorithm. The dynamic CBG is analyzed under the framework of combinatorial bandit and bandit with knapsacks. We first convert the dynamic CBG with budget constraint to a path planning problem on a graph. We then devise an efficient dynamic policy for the learner that uses a combinatorial bandit algorithm Edge on the path planning graph as a subroutine for another algorithm LagrangeBwK. It is shown that under the proposed policy, the learner's regret is bounded with high probability by a term sublinear in time horizon $T$ and polynomial with respect to other parameters.