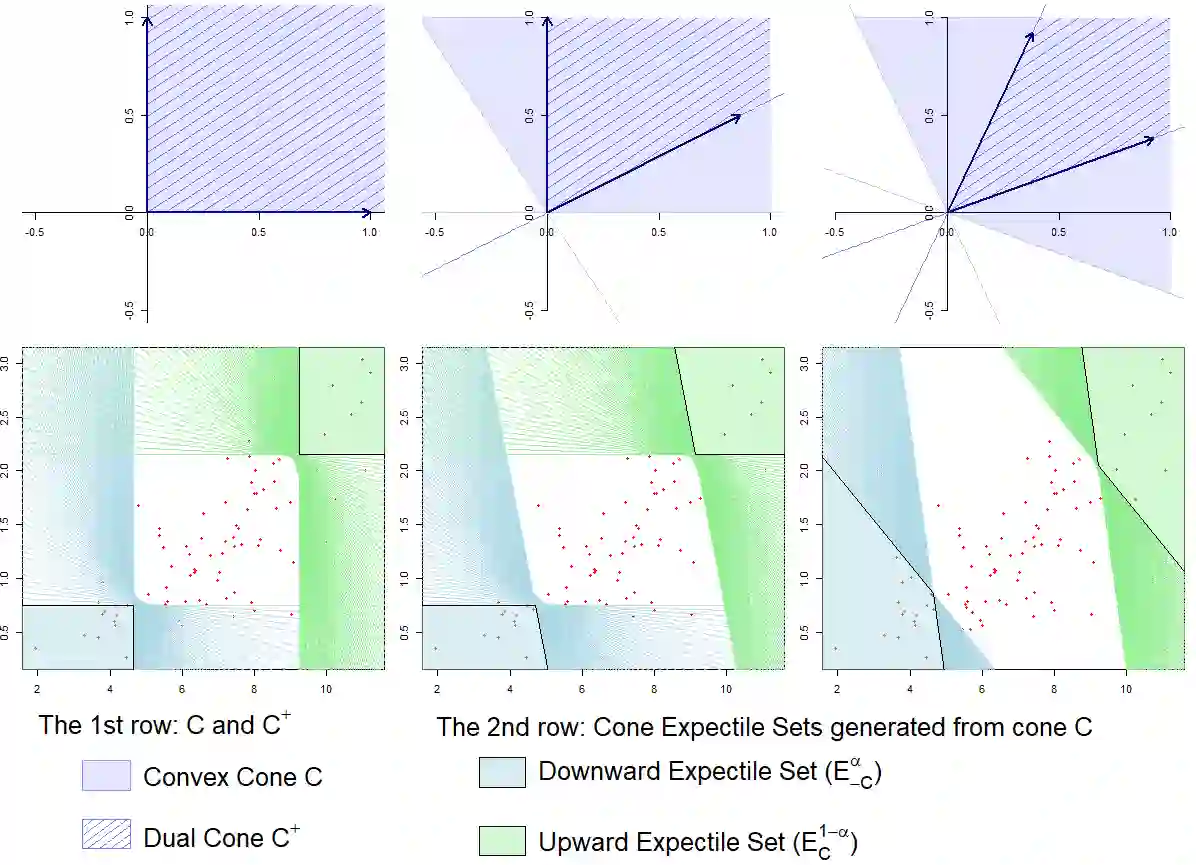
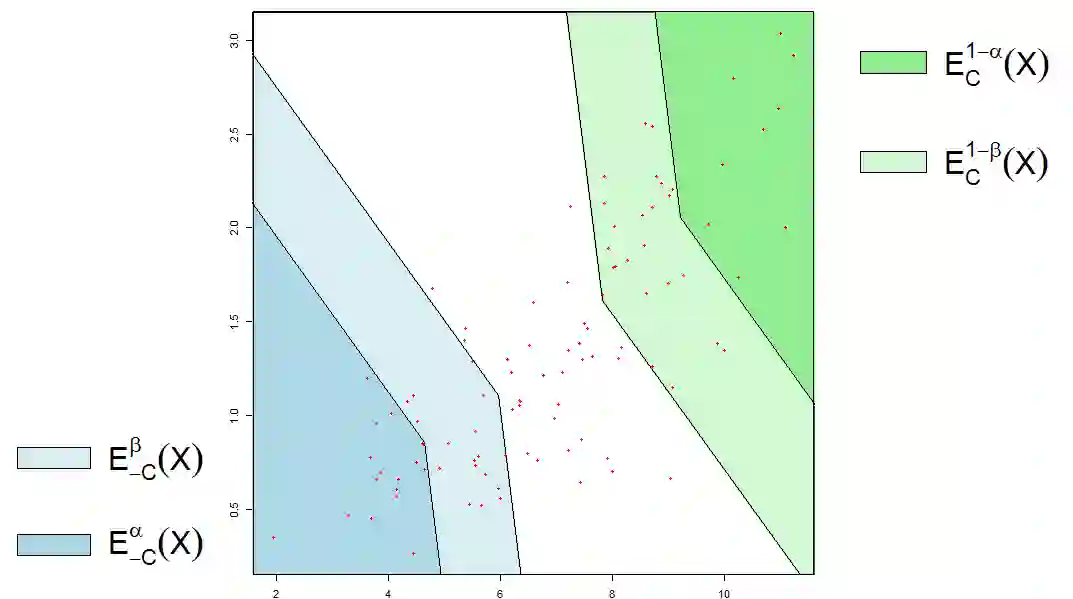
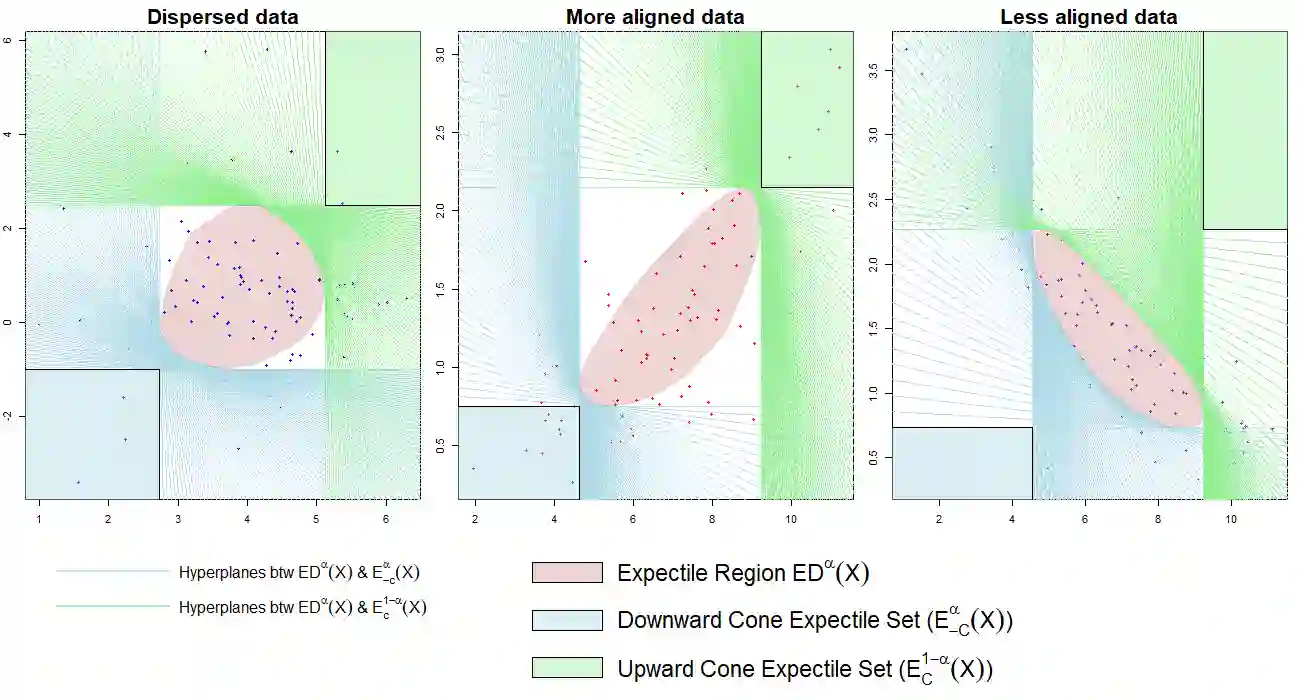
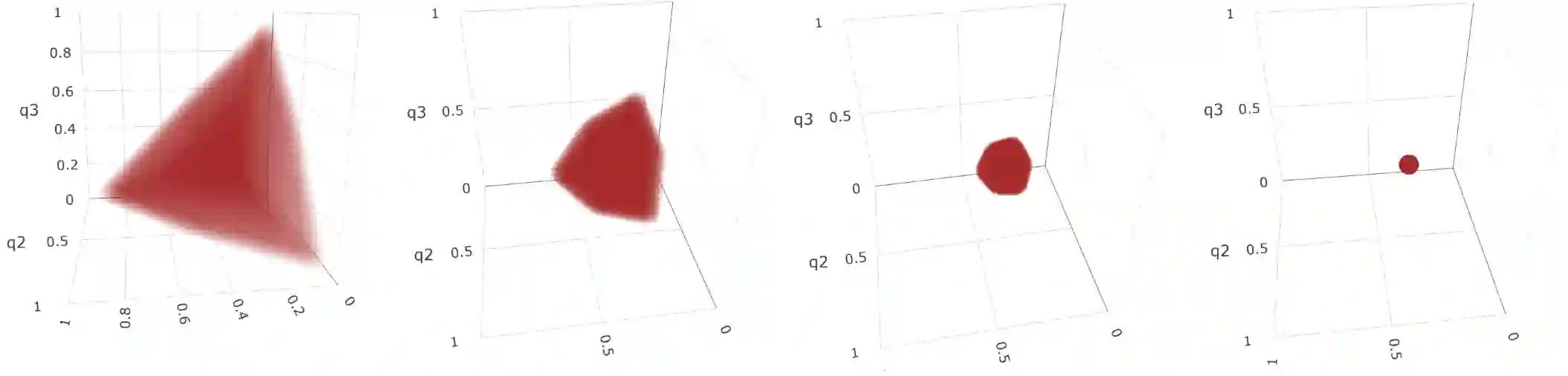
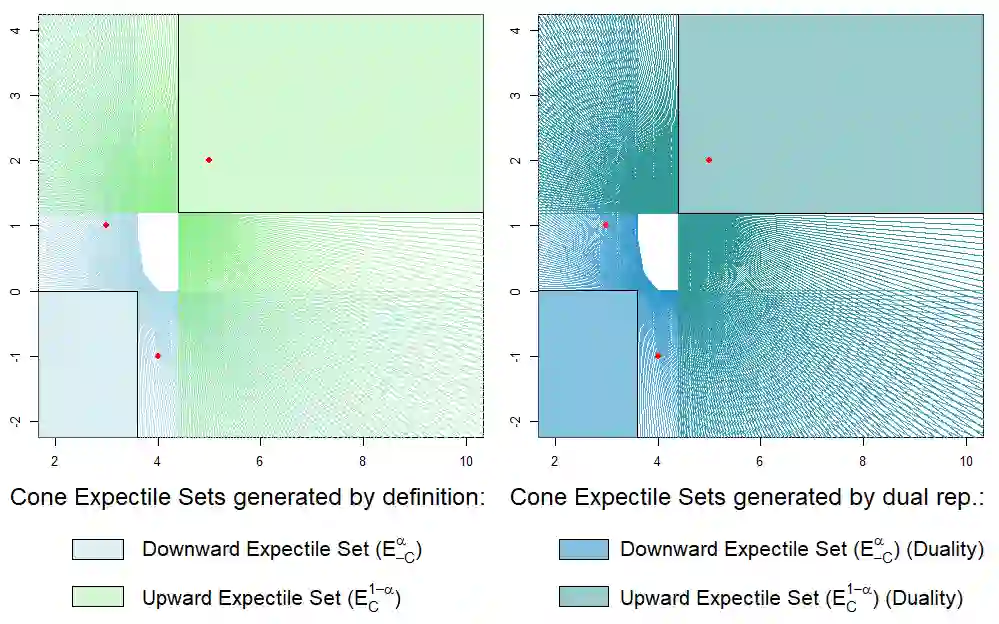
Recently defined expectile regions capture the idea of centrality with respect to a multivariate distribution, but fail to describe the tail behavior while it is not at all clear what should be understood by a tail of a multivariate distribution. Therefore, cone expectile sets are introduced which take into account a vector preorder for the multi-dimensional data points. This provides a way of describing and clustering a multivariate distribution/data cloud with respect to an order relation. Fundamental properties of cone expectiles including dual representations of both expectile regions and cone expectile sets are established. It is shown that set-valued sublinear risk measures can be constructed from cone expectile sets in the same way as in the univariate case. Inverse functions of cone expectiles are defined which should be considered as rank functions rather than depth functions. Finally, expectile orders for random vectors are introduced and characterized via expectile rank functions.
翻译:暂无翻译