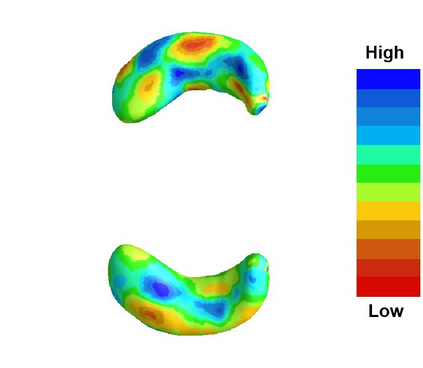
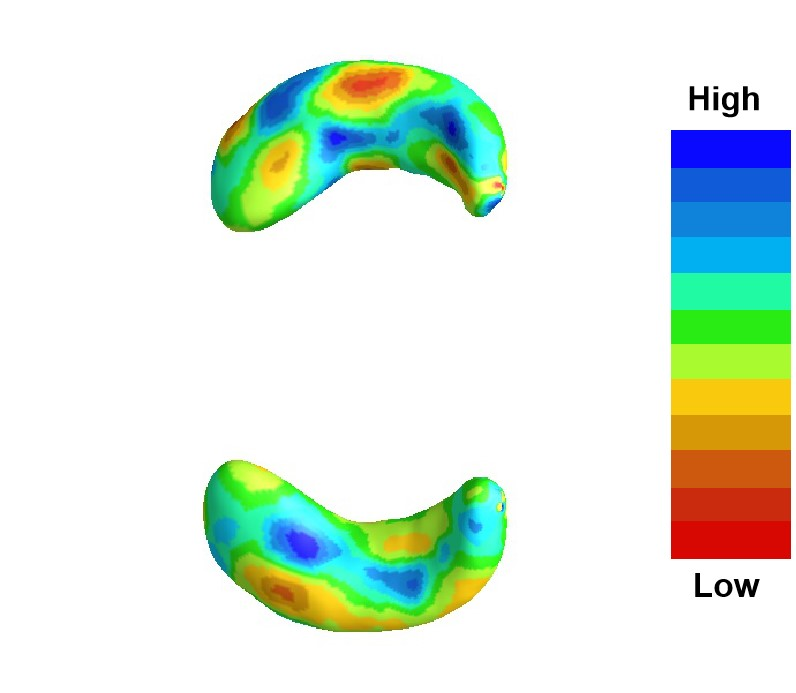
Independence analysis is an indispensable step before regression analysis to find out essential factors that influence the objects. With many applications in machine Learning, medical Learning and a variety of disciplines, statistical methods of measuring the relationship between random variables have been well studied in vector spaces. However, there are few methods developed to verify the relation between random elements in metric spaces. In this paper, we present a novel index called metric distributional discrepancy (MDD) to measure the dependence between a random element $X$ and a categorical variable $Y$, which is applicable to the medical image and genetic data. The metric distributional discrepancy statistics can be considered as the distance between the conditional distribution of $X$ given each class of $Y$ and the unconditional distribution of $X$. MDD enjoys some significant merits compared to other dependence-measures. For instance, MDD is zero if and only if $X$ and $Y$ are independent. MDD test is a distribution-free test since there is no assumption on the distribution of random elements. Furthermore, MDD test is robust to the data with heavy-tailed distribution and potential outliers. We demonstrate the validity of our theory and the property of the MDD test by several numerical experiments and real data analysis.
翻译:独立分析是回归分析之前一个不可或缺的步骤,以找出影响物体的基本因素。在机器学习、医学学习和各种学科的许多应用中,测量随机变数之间关系的统计方法已经在矢量空间中进行了仔细研究,然而,在核实公吨空间随机元素之间的关系方面,没有开发出什么方法。在本文件中,我们提出了一个名为“衡量随机元素X美元和绝对变量Y美元之间依赖性的新指数,该指数适用于医学图象和遗传数据。衡量分布差异的数据可被视为按每类Y美元和无条件分配X美元的条件分配的X美元之间的距离。与其它依赖度衡量尺度相比,MDD具有一些显著的优点。例如,如果且只有在X美元和Y美元是独立的,MDD是零,那么MDD是无分布差异的测试,因为对随机元素的分布没有假设。此外,MDDD测试对于具有大量尾量分布和潜在外值的数据是可靠的。我们通过数项实验来证明我们理论的正确性以及MDDD测试的真性。