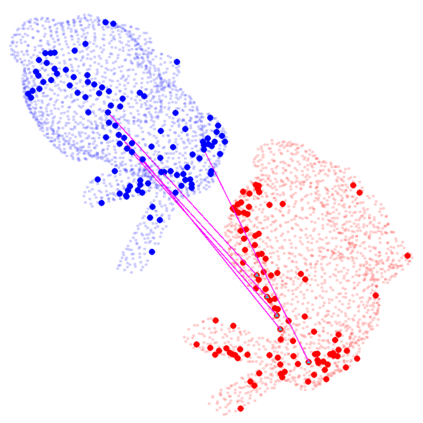
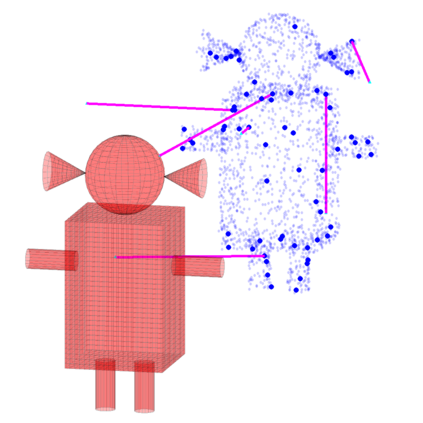
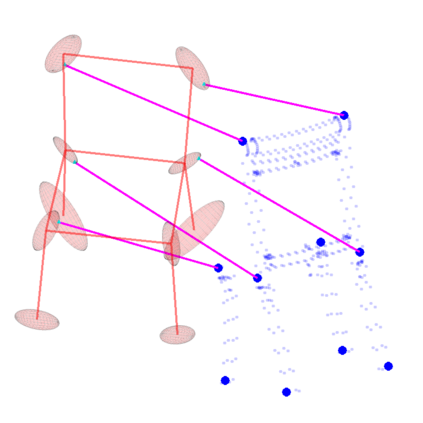
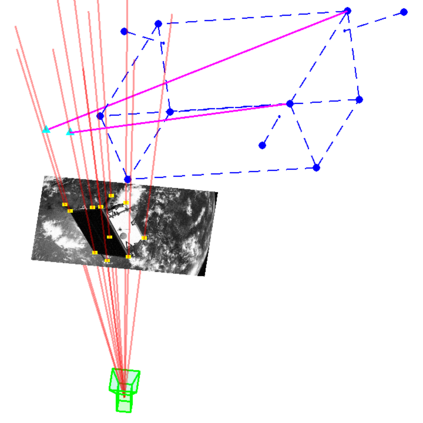
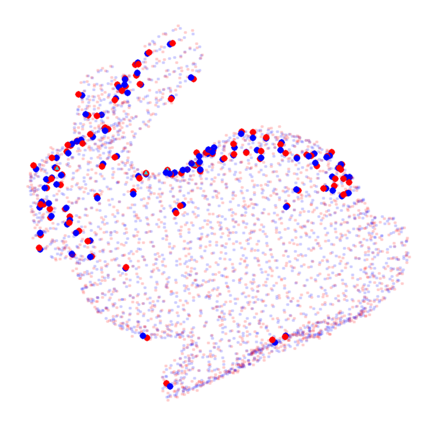
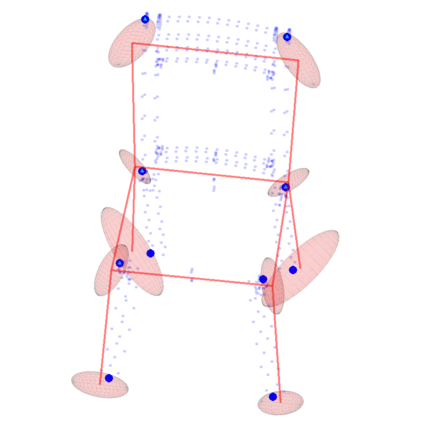
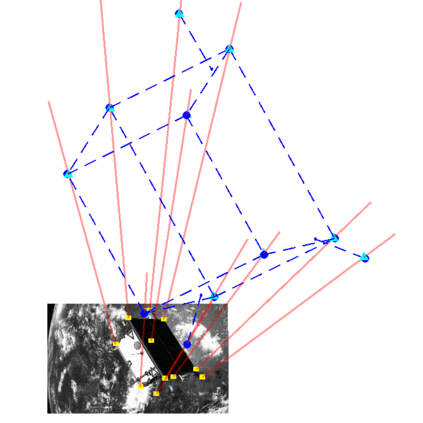
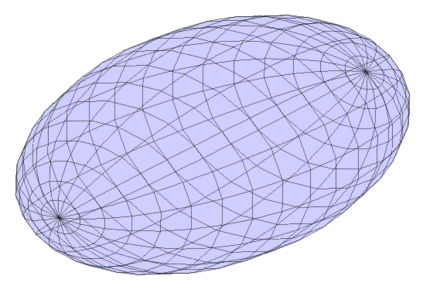
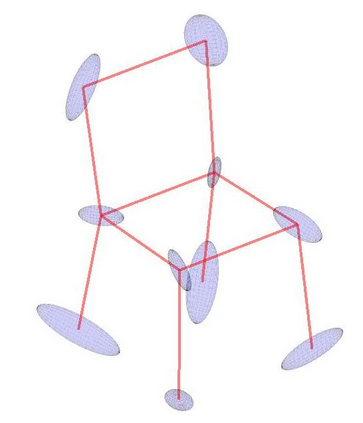
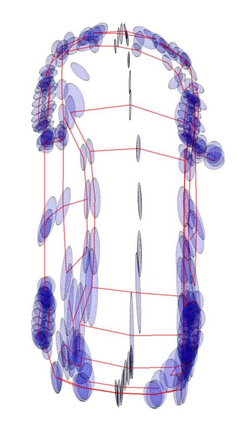
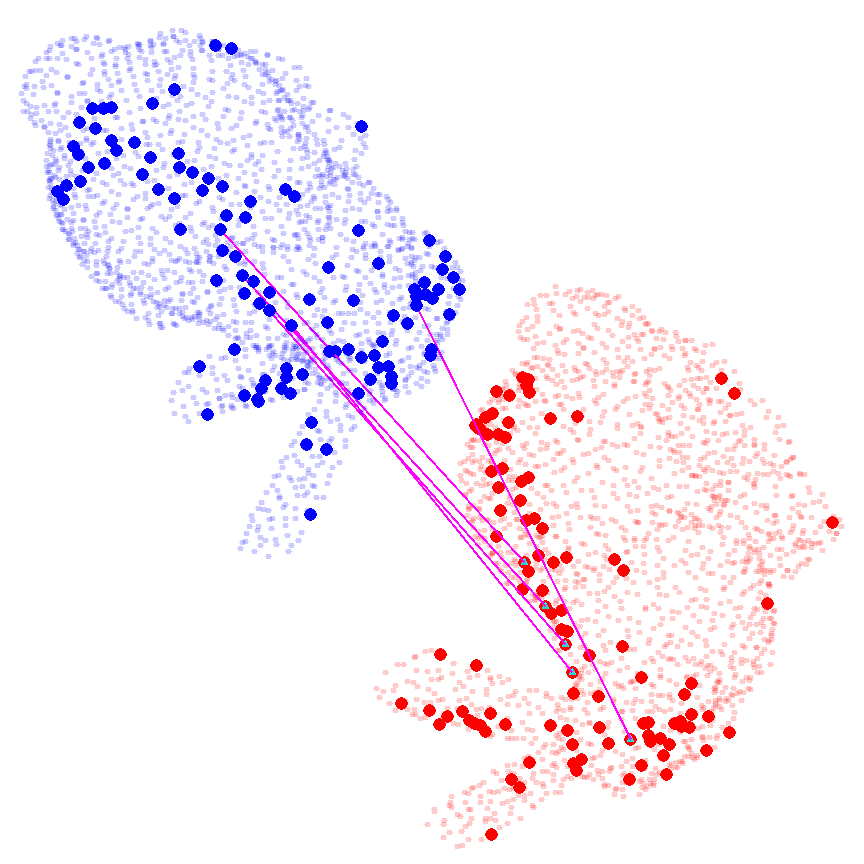
We study the problem of aligning two sets of 3D geometric primitives given known correspondences. Our first contribution is to show that this primitive alignment framework unifies five perception problems including point cloud registration, primitive (mesh) registration, category-level 3D registration, absolution pose estimation (APE), and category-level APE. Our second contribution is to propose DynAMical Pose estimation (DAMP), the first general and practical algorithm to solve primitive alignment problem by simulating rigid body dynamics arising from virtual springs and damping, where the springs span the shortest distances between corresponding primitives. Our third contribution is to apply DAMP to the five perception problems in simulated and real datasets and demonstrate (i) DAMP always converges to the globally optimal solution in the first three problems with 3D-3D correspondences; (ii) although DAMP sometimes converges to suboptimal solutions in the last two problems with 2D-3D correspondences, with a simple scheme for escaping local minima, DAMP almost always succeeds. Our last contribution is to demystify the surprising empirical performance of DAMP and formally prove a global convergence result in the case of point cloud registration by charactering local stability of the equilibrium points of the underlying dynamical system.
翻译:我们研究将已知通信中的两组三维几何原始体相匹配的问题。 我们的第一个贡献是,我们研究将已知通信中的两组三维几何原始体相匹配的问题。 我们的第一个贡献是,这个原始的调整框架将五种认知问题,包括点云登记、原始(黑)登记、类3D登记、类别3D登记、和解产生估计(APE)和类别一级APE。我们的第二个贡献是提出DynAMical Pose估计(DAMP),这是通过模拟虚拟泉源和阻塞产生的僵硬体动态来解决原始调节问题的第一个一般和实用的算法,在虚拟泉源之间距离最短的距离中,泉源几乎总是能够成功。我们的第三个贡献是将DAMP在模拟和真实数据集中的五个认知问题应用DAMMP,并展示:(一) DAMP在前三个问题中总是会与3D-3D通信通信中的全球最佳解决方案趋同;(二) 虽然DAMP有时会与最后两个问题相交错的次优化解决方案相融合,其简单的办法是逃避当地微型,DAMP几乎总是会成功。 我们的最后贡献是消除DAMMP的惊人实证性表现,并通过当地稳定稳定的云性结果。