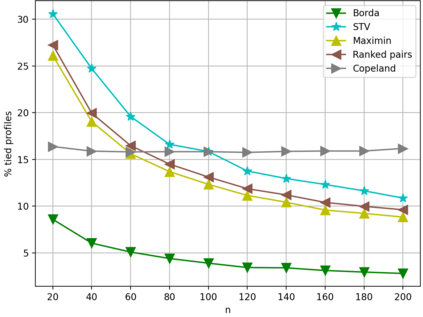
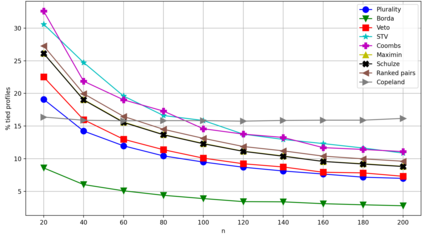
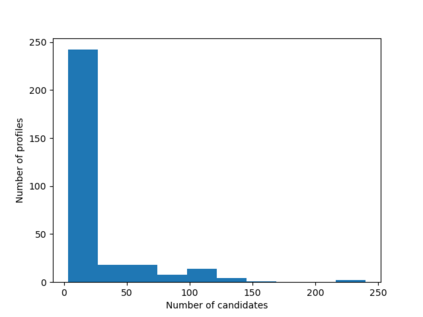
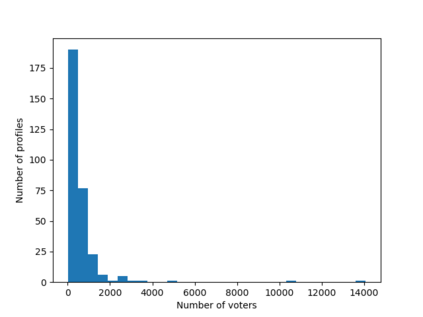
Understanding the likelihood for an election to be tied is a classical topic in many disciplines including social choice, game theory, political science, and public choice. Despite a large body of literature and the common belief that ties are rare, little is known about how rare ties are in large elections except for a few simple positional scoring rules under the i.i.d. uniform distribution over the votes, known as the Impartial Culture (IC) in social choice. In particular, little progress was made after Marchant explicitly posed the likelihood of k-way ties under IC as an open question in 2001. We give an asymptotic answer to the open question for a wide range of commonly studied voting rules under a model that is much more general and realistic than i.i.d. models (especially IC) -- the smoothed social choice framework by Xia that was inspired by the celebrated smoothed complexity analysis by Spielman and Teng. We prove dichotomy theorems on the smoothed likelihood of ties under positional scoring rules, edge-order-based rules, and some multi-round score-based elimination rules, which include commonly studied voting rules such as plurality, Borda, veto, maximin, Copeland, ranked pairs, Schulze, STV, and Coombs as special cases. We also complement the theoretical results by experiments on synthetic data and real-world rank data on Preflib. Our main technical tool is an improved dichotomous characterization on the smoothed likelihood for a Poisson multinomial variable to be in a polyhedron, which is proved by exploring the interplay between the V-representation and the matrix representation of polyhedra and might be of independent interest.
翻译:了解选举被绑在一起的可能性是许多学科的一个古典话题,包括社会选择、游戏理论、政治学和公众选择。尽管有大量文献和普遍认为联系很少,但对于大选举中联系的罕见程度却知之甚少,除非根据i.i.d.d. 统一分配选票的统一规则,即所谓的社会选择中的公正文化(IC),在社会选择中被称作“公正文化(IC) ” 。特别是,在三月之后,几乎没有取得什么进展,从而明确将IC下k-way联系的可能性作为2001年的一个开放问题。我们给出了一个无端的答案,问一个开放的问题,即根据一种比i.d. 模式更一般和现实得多的通常研究的可变投票规则。 模型(特别是IC)是Xia 的平滑的社会选择框架,这个框架受到Spielman和Teng的庆祝的简单复杂分析的启发。 事实证明,在立场评分规则、基于边际规则的多级代表制规则以及一些基于分数的取消规则之间,这包括共同研究的投票规则,例如Schodrodrodro devo disal-reval ex、Bal-cal-calstalbalbisleval be cal be cal be cal be cal be cal ex ex exaldaldaldaldal ex ex ex ex ex ex ex ex ex ex ex ex ex exbus ex ex exbus ex ex ex ex exitalviolviolviolviolviolvicus ex exitald ex ex ex ex exbus exbus ex ex ex ex ex exbaldaldal ex ex ex ex ex ex ex ex ex ex ex ex ex exbaldaldaldal ex ex ex ex ex ex ex ex ex, ex ex ex ex ex ex ex ex ex ex ex ex ex exal ex ex ex ex ex ex ex ex ex