Bayes Factor Asymptotics for Variable Selection in the Gaussian Process Framework

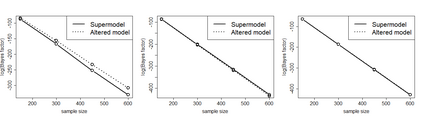
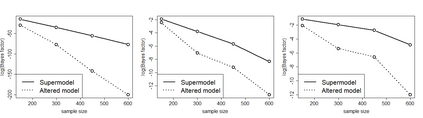
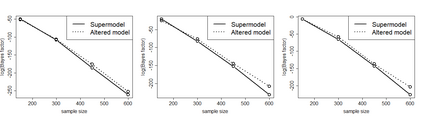
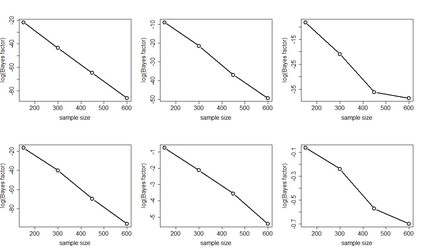
Although variable selection is one of the most popular areas of modern statistical research, much of its development has taken place in the classical paradigm compared to the Bayesian counterpart. Somewhat surprisingly, both the paradigms have focussed almost completely on linear models, in spite of the vast scope offered by the model liberation movement brought about by modern advancements in studying real, complex phenomena. In this article, we investigate general Bayesian variable selection in models driven by Gaussian processes, which allows us to treat linear, non-linear and nonparametric models, in conjunction with even dependent setups, in the same vein. We consider the Bayes factor route to variable selection, and develop a general asymptotic theory for the Gaussian process framework in the "large p, large n" settings even with p>>n, establishing almost sure exponential convergence of the Bayes factor under appropriately mild conditions. The fixed p setup is included as a special case. To illustrate, we apply our general result to variable selection in linear regression, Gaussian process model with squared exponential covariance function accommodating the covariates, and a first order autoregressive process with time-varying covariates. We also follow up our theoretical investigations with ample simulation experiments in the above regression contexts and variable selection in a real, riboflavin data consisting of 71 observations but 4088 covariates. For implementation of variable selection using Bayes factors, we develop a novel and effective general-purpose transdimensional, transformation based Markov chain Monte Carlo algorithm, which has played a crucial role in our simulated and real data applications.