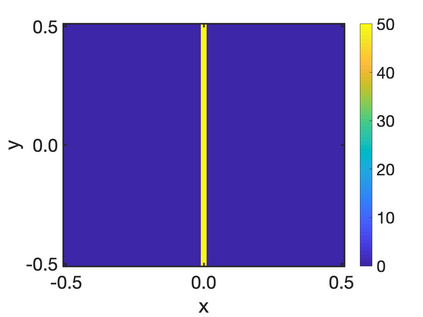
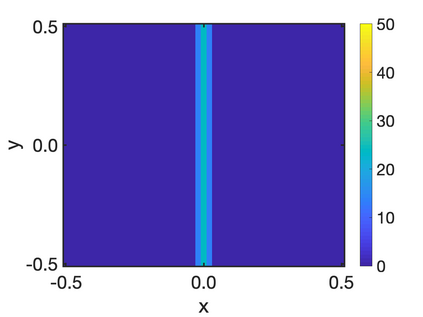
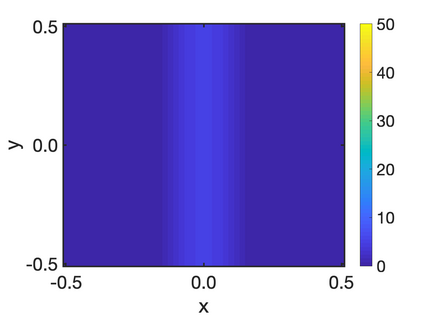
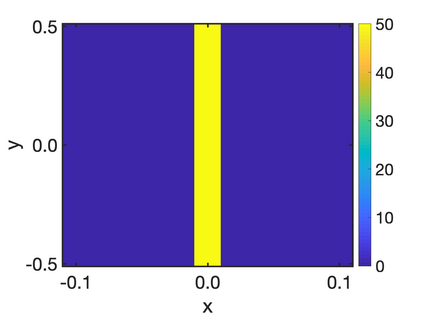
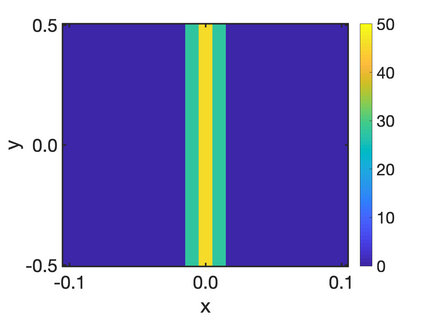
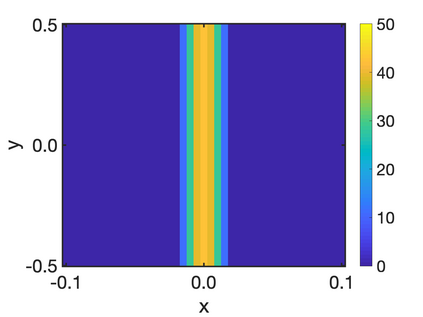
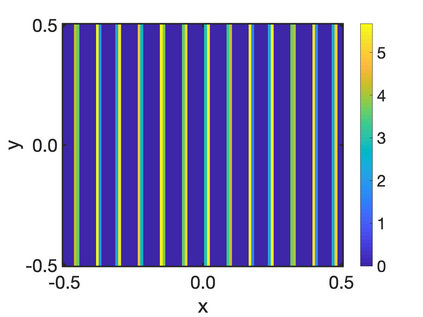
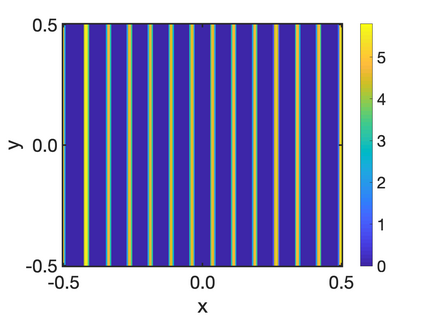
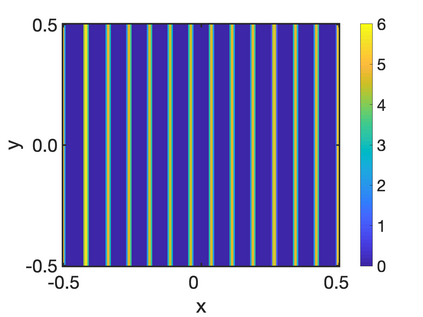
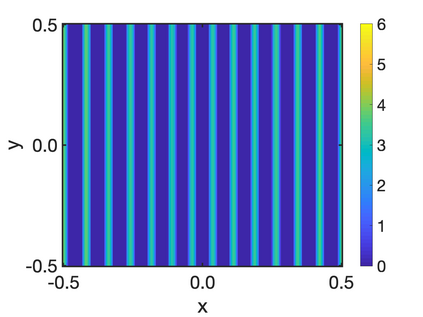
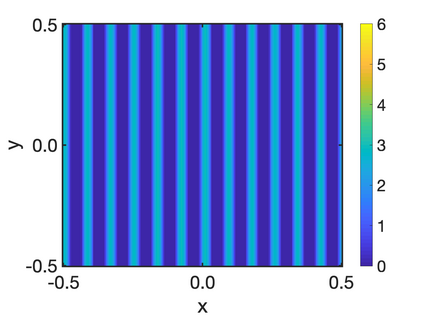
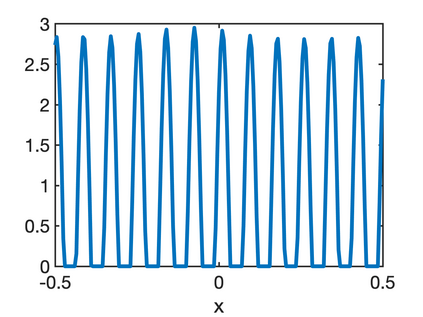
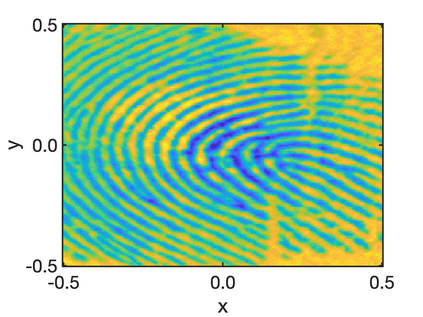
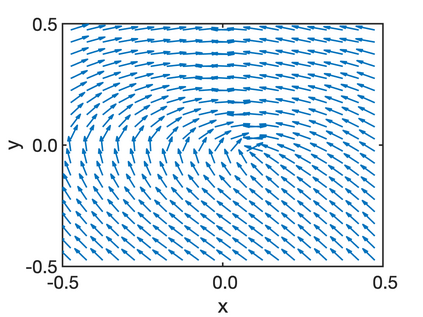
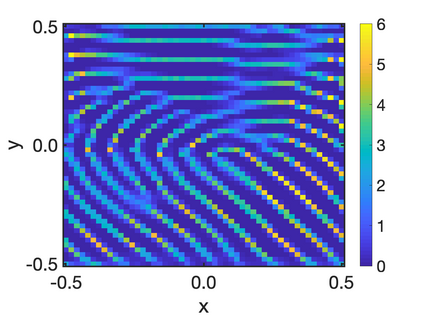
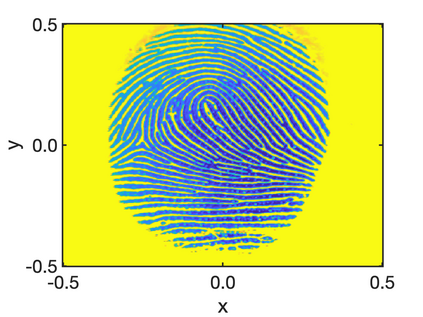
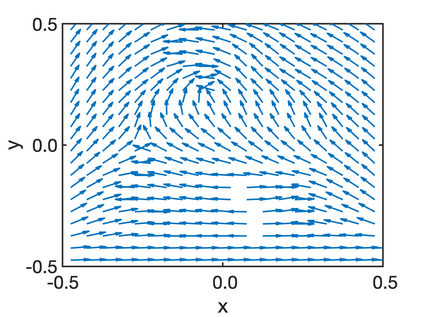
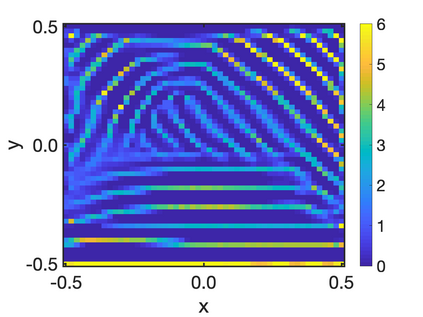
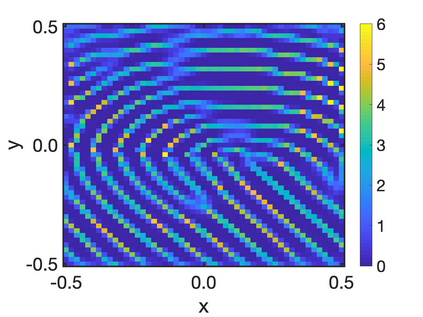
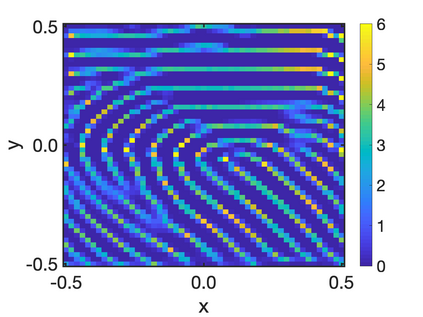
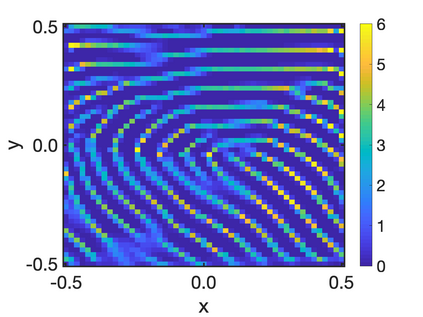
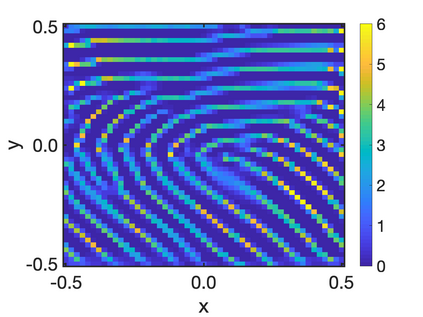
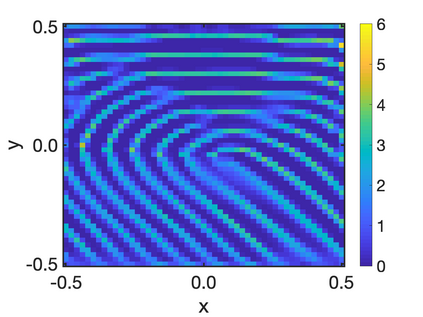
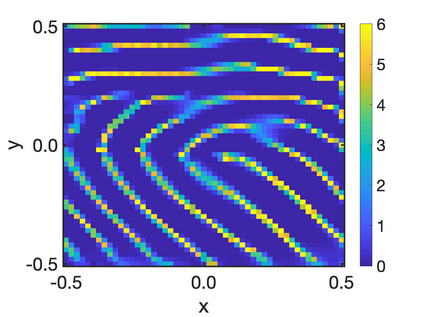
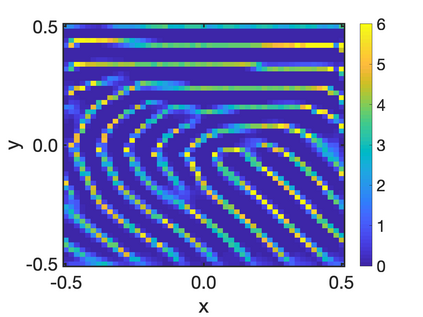
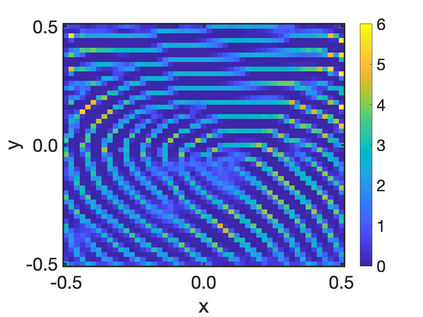
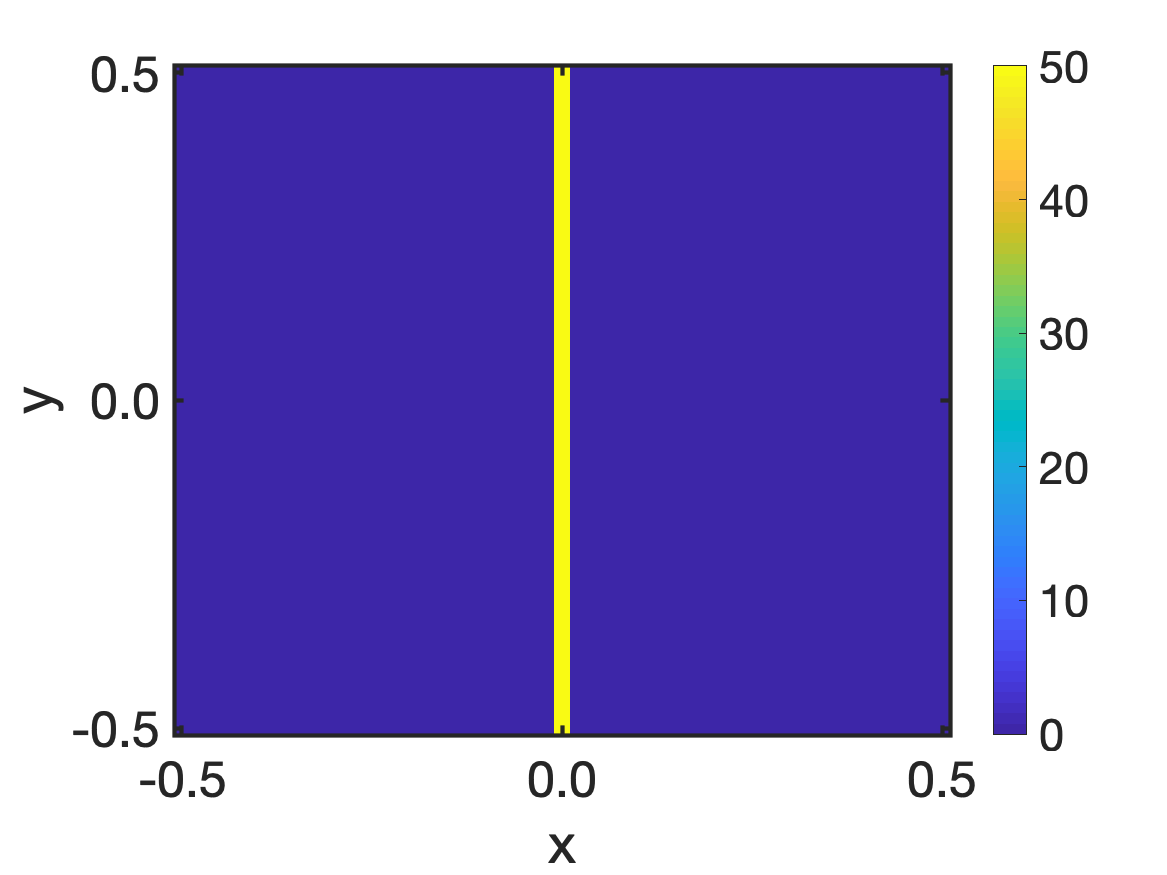
In this paper, we study the equilibria of an anisotropic, nonlocal aggregation equation with nonlinear diffusion which does not possess a gradient flow structure. Here, the anisotropy is induced by an underlying tensor field. Anisotropic forces cannot be associated with a potential in general and stationary solutions of anisotropic aggregation equations generally cannot be regarded as minimizers of an energy functional. We derive equilibrium conditions for stationary line patterns in the setting of spatially homogeneous tensor fields. The stationary solutions can be regarded as the minimizers of a regularised energy functional depending on a scalar potential. A dimension reduction from the two- to the one-dimensional setting allows us to study the associated one-dimensional problem instead of the two-dimensional setting. We establish $\Gamma$-convergence of the regularised energy functionals as the diffusion coefficient vanishes, and prove the convergence of minimisers of the regularised energy functional to minimisers of the non-regularised energy functional. Further, we investigate properties of stationary solutions on the torus, based on known results in one spatial dimension. Finally, we prove weak convergence of a numerical scheme for the numerical solution of the anisotropic, nonlocal aggregation equation with nonlinear diffusion and any underlying tensor field, and show numerical results.
翻译:在本文中, 我们研究非本地总和等离子体的平衡性, 且不具有梯度流结构的非线性扩散。 这里, 亚异性激素是由一个深点引发的。 亚异性力量不能与一般和固定的反异性聚合方程式的潜在潜在解决办法相联系, 一般来说不能被视为能量功能的最小化因素。 我们为在空间上同质的抗拉场设置固定的线型模式提供均衡条件。 固定性解决方案可以被视为一个固定化能源功能的最小化因素, 取决于星际潜力。 从二维到一维环境的尺寸的减少使我们能够研究相关的一维问题, 而不是二维环境的设置。 我们为正常化能源功能的元值设定了$\Gamma$- 趋同力, 证明常规化能源功能的最小化因素与非常规性能源功能的最小化因素相融合。 此外, 我们根据已知的空间扩散结果, 在已知的一维度上固定化的能源功能的特性, 从一个已知的一维度到一维度的一维度的维度上进行研究。 最后, 我们证明一个最小化的数的数值的数值的数值的数值的数值的数值的数值的组合。