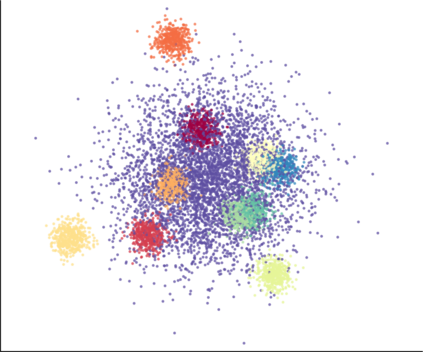
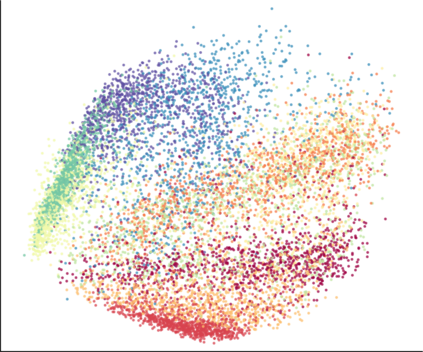
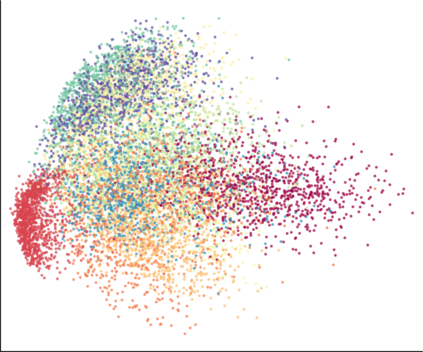
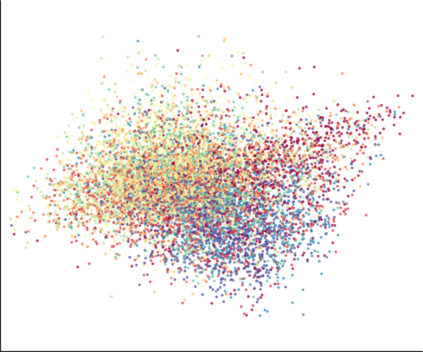
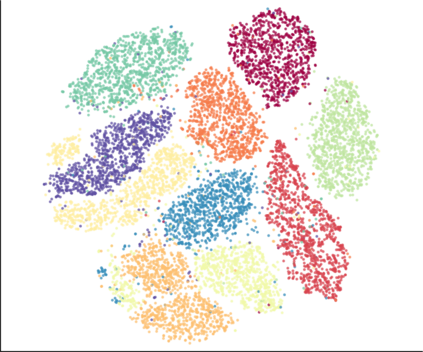
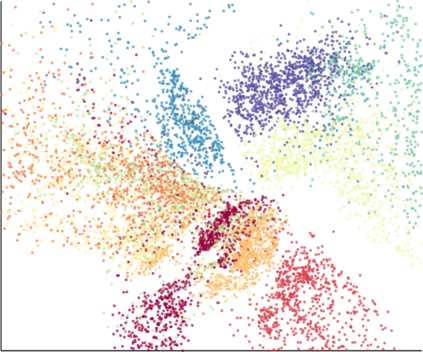
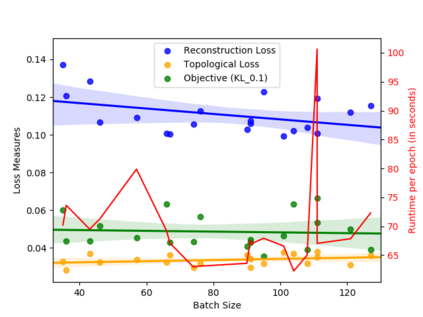
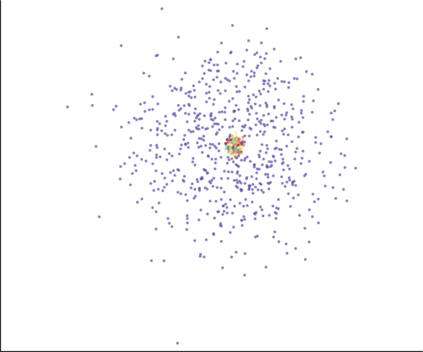
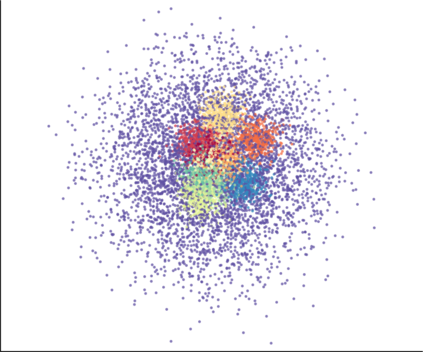
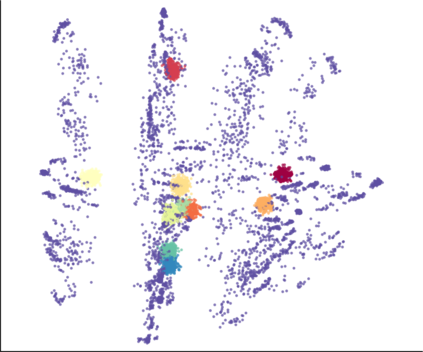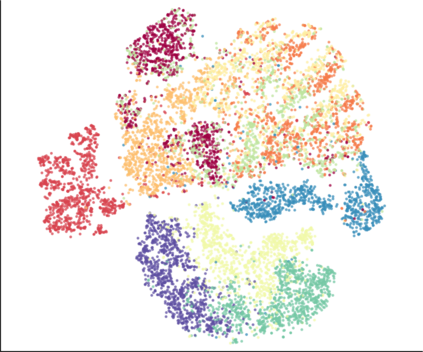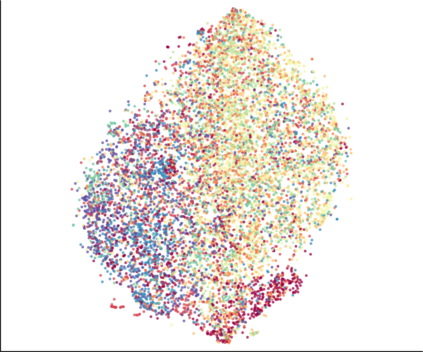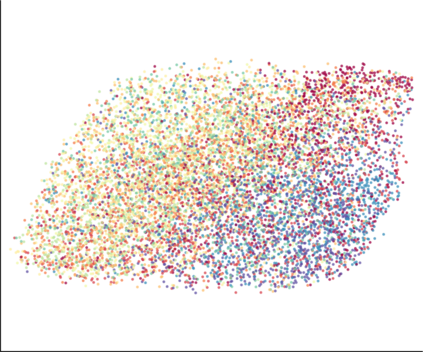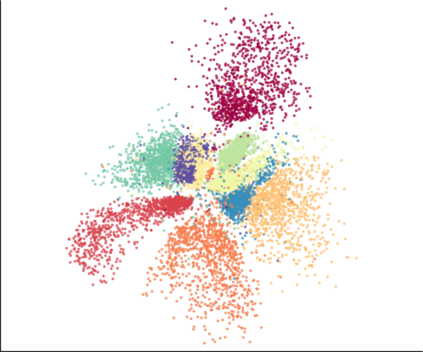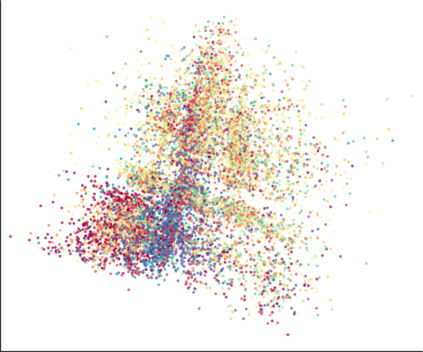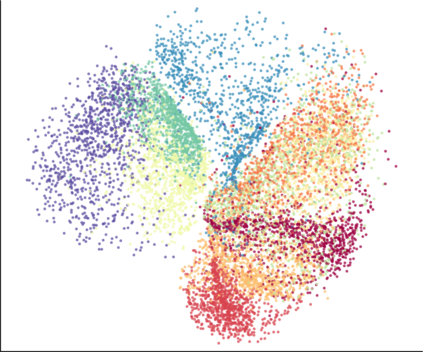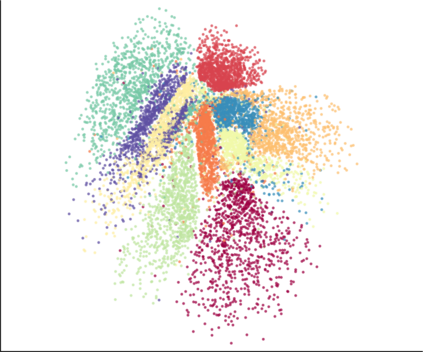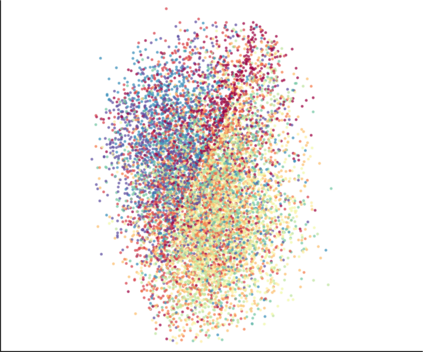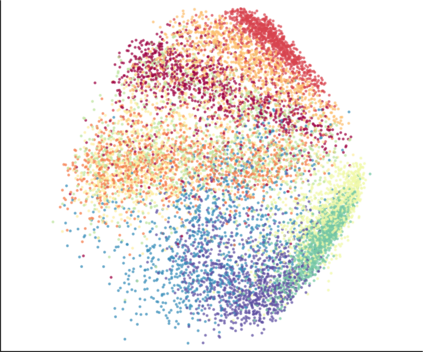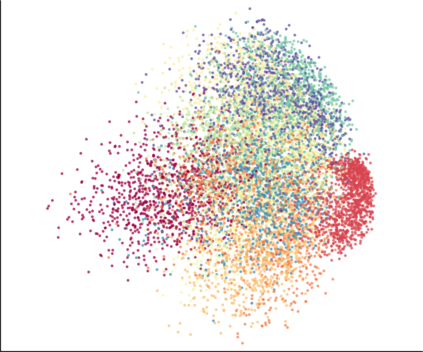We propose a novel approach for preserving topological structures of the input space in latent representations of autoencoders. Using persistent homology, a technique from topological data analysis, we calculate topological signatures of both the input and latent space to derive a topological loss term. Under weak theoretical assumptions, we construct this loss in a differentiable manner, such that the encoding learns to retain multi-scale connectivity information. We show that our approach is theoretically well-founded and that it exhibits favourable latent representations on a synthetic manifold as well as on real-world image data sets, while preserving low reconstruction errors.
翻译:我们提出了一种新颖的方法来保护输入空间的表层结构,将其保存在自动转换器的潜在代表中。我们利用持续同质学(一种来自地形数据分析的技术)来计算输入空间和潜在空间的表层特征,以得出一个表层损失的术语。在薄弱的理论假设下,我们用不同的方式构建了这一损失,这样编码就可以学会保留多尺度的连接信息。我们表明,我们的方法在理论上是有充分根据的,在合成元体和真实世界图像数据集上都表现出有利的潜在特征,同时保留了较低的重建错误。