Nonlinear Unknown Input Observability and Unknown Input Reconstruction: The General Analytical Solution

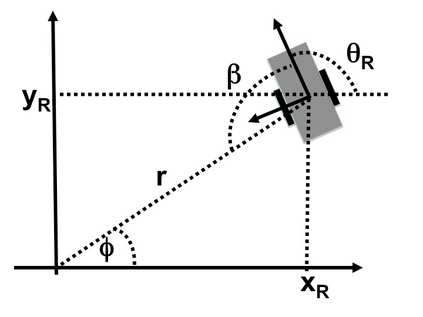
Observability is a fundamental structural property of any dynamic system and describes the possibility of reconstructing the state that characterizes the system from observing its inputs and outputs. Despite the huge effort made to study this property and to introduce analytical criteria able to check whether a dynamic system satisfies this property or not, there is no general analytical criterion to automatically check the state observability when the dynamics are also driven by unknown inputs. Here, we introduce the general analytical solution of this fundamental problem, often called the unknown input observability problem. This paper provides the general analytical solution of this problem, namely, it provides the systematic procedure, based on automatic computation (differentiation and matrix rank determination), that allows us to automatically check the state observability even in the presence of unknown inputs. A first solution of this problem was presented in the second part of the book: "Observability: A New Theory Based on the Group of Invariance" [45]. The solution presented by this paper completes the previous solution in [45]. In particular, the new solution exhaustively accounts for the systems that do not belong to the category of the systems that are canonic with respect to their unknown inputs. The new solution is also provided in the form of a new algorithm. A further novelty with respect to the algorithm provided in [45] consists of a new convergence criterion that holds in all the cases (the convergence criterion of the algorithm provided in [45] can fail in some cases). Finally, we also provide the answer to the problem of unknown input reconstruction which is intimately related to the problem of state observability. We illustrate the implementation of the new algorithm by studying a nonlinear system in the framework of visual-inertial sensor fusion.