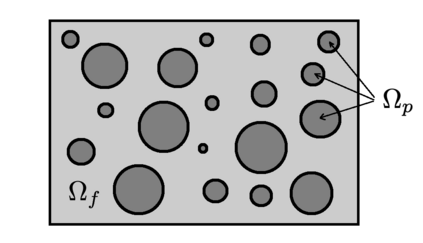
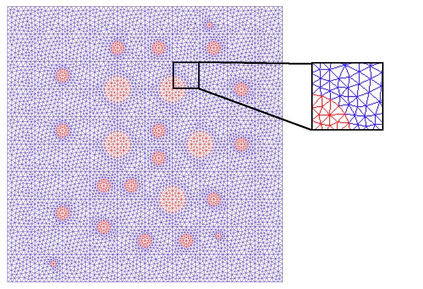
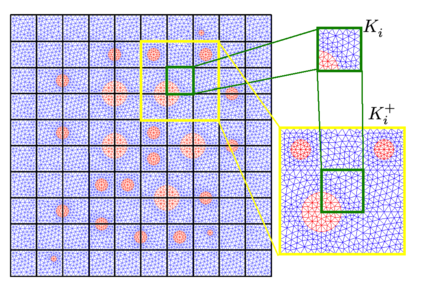
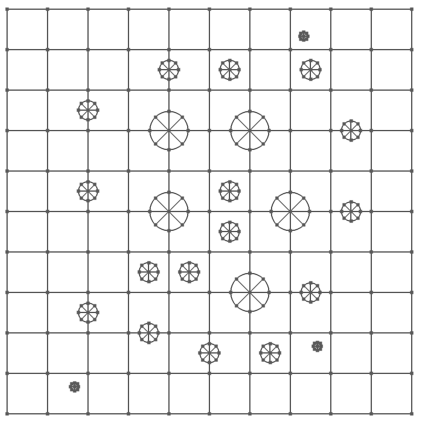
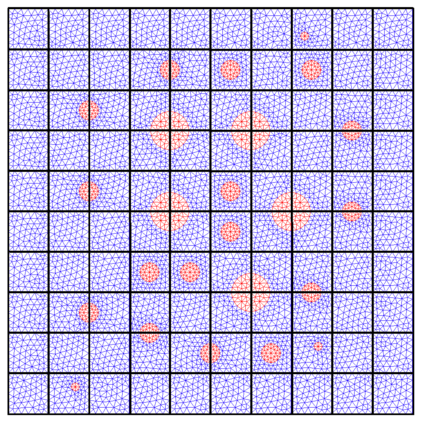
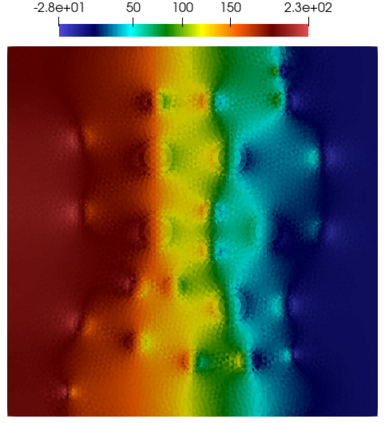
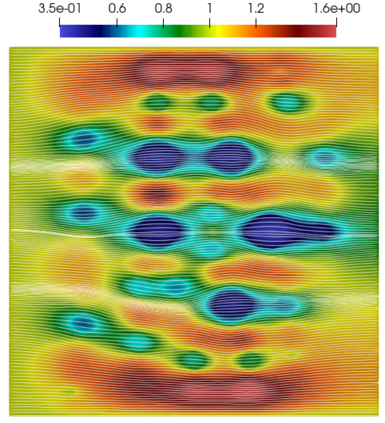
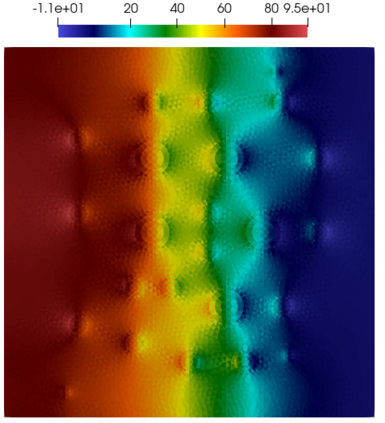
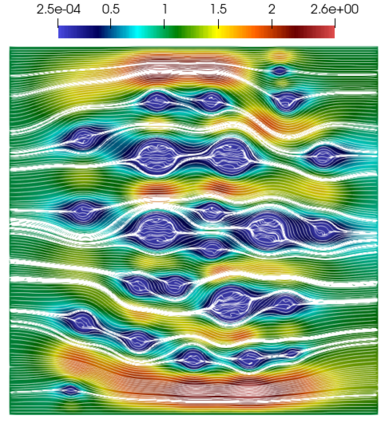
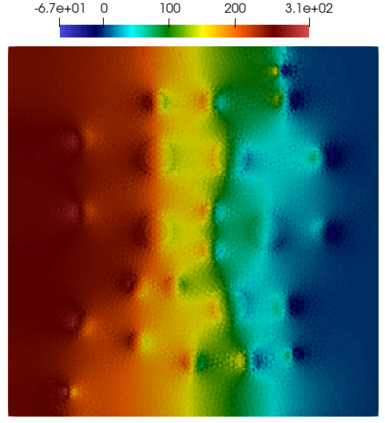
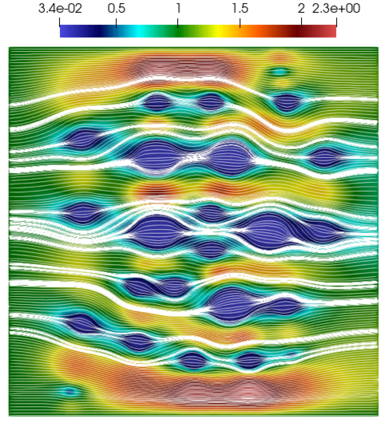
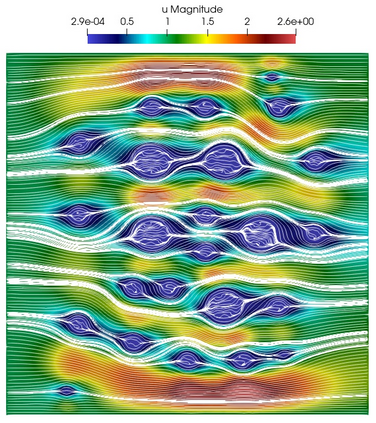
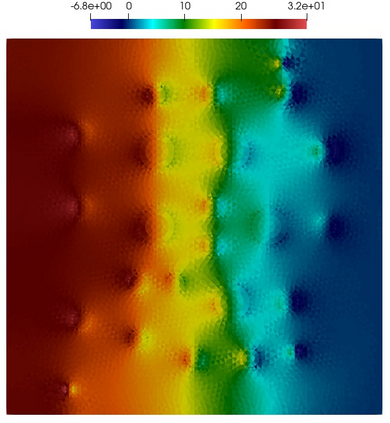
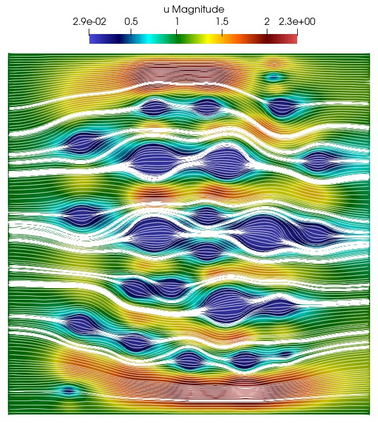
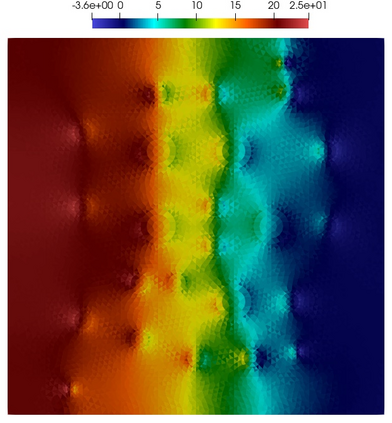
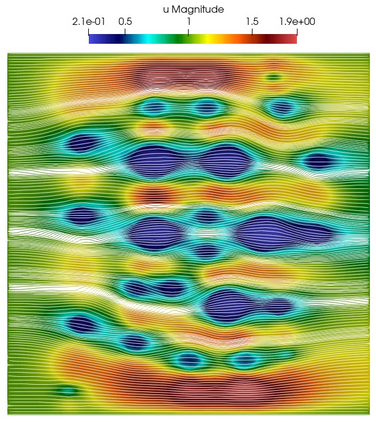
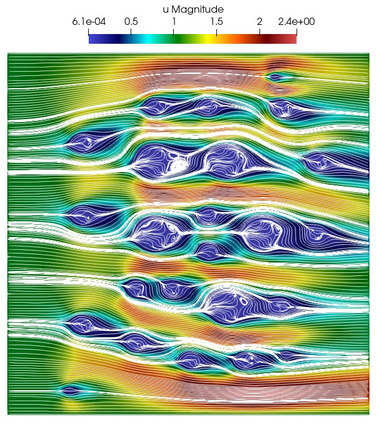
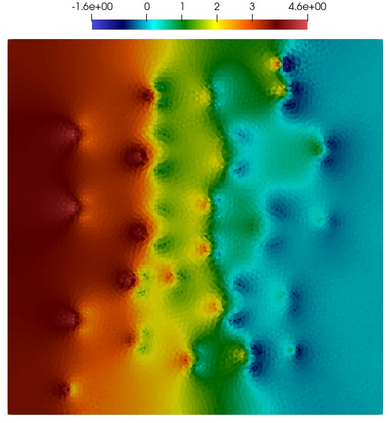
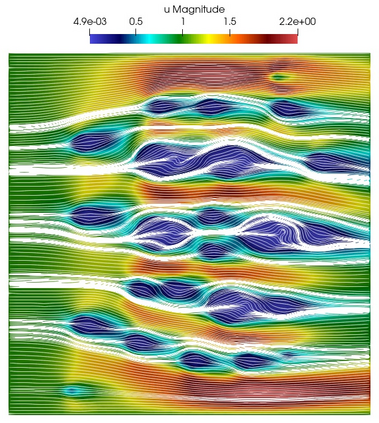
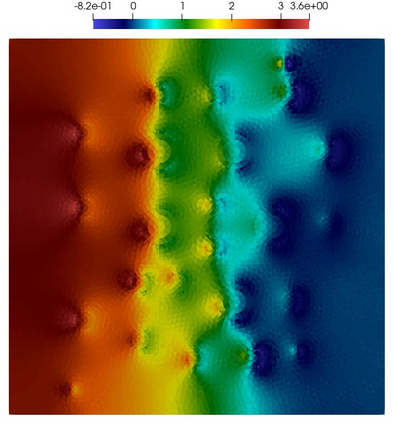
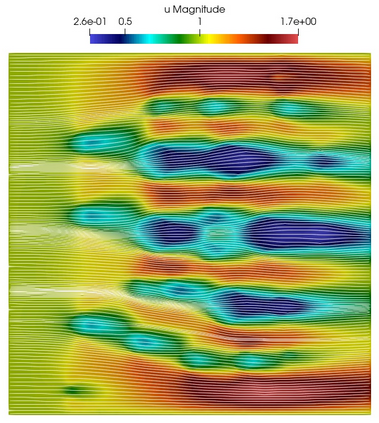
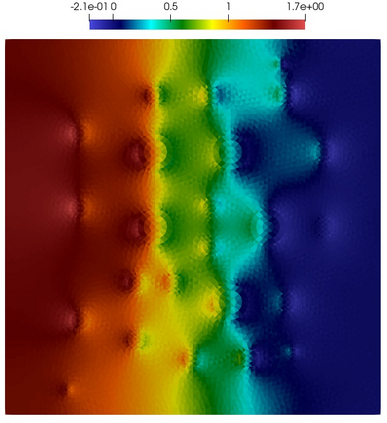
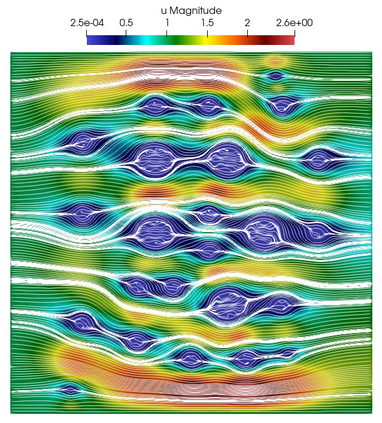
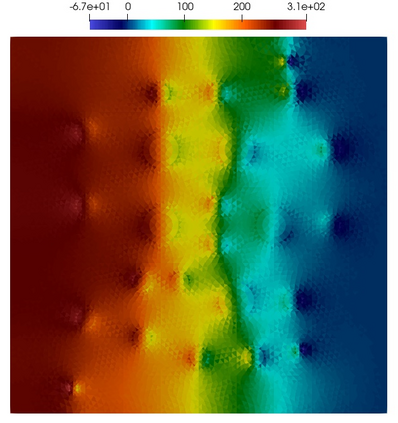
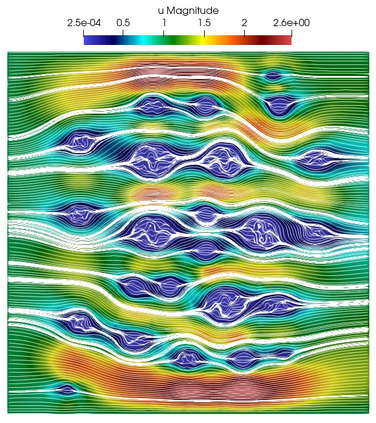
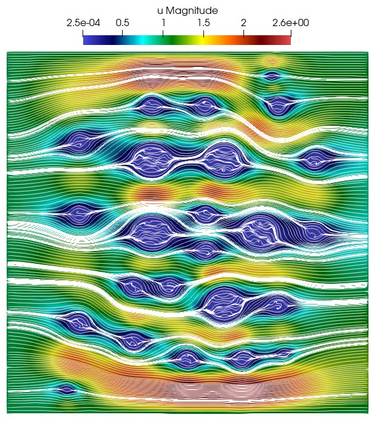
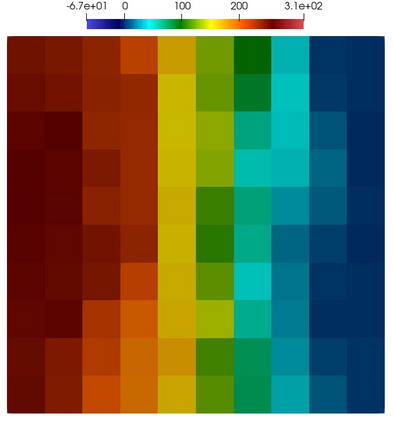
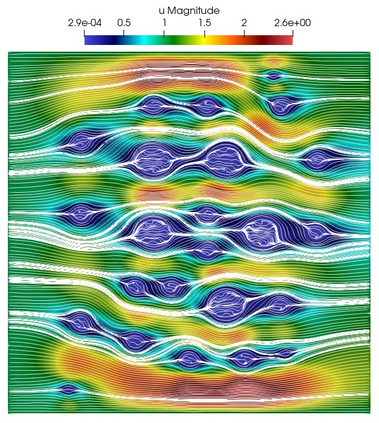
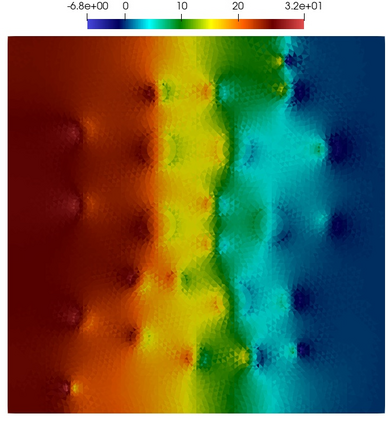
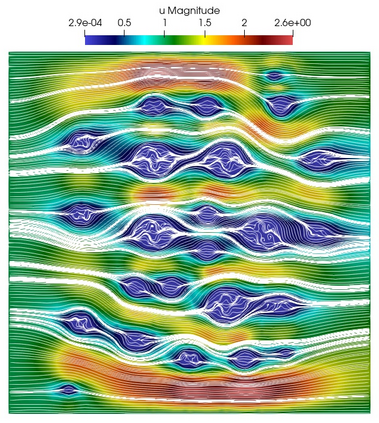
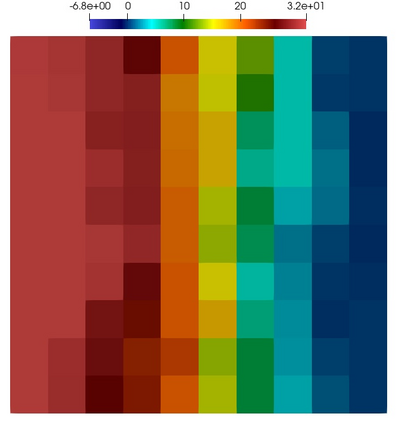
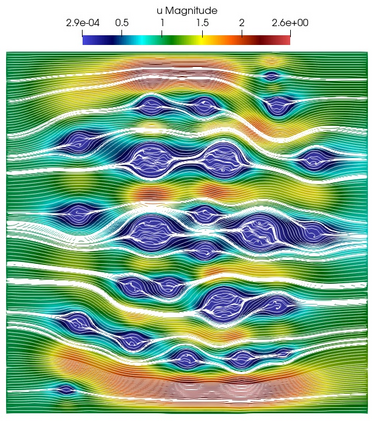
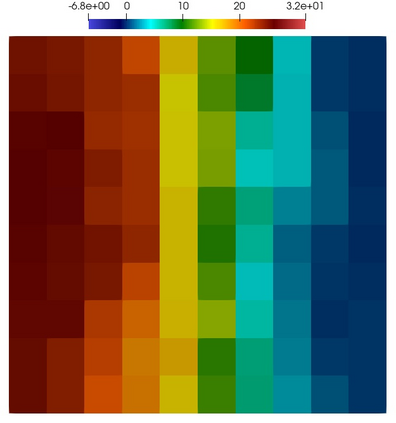
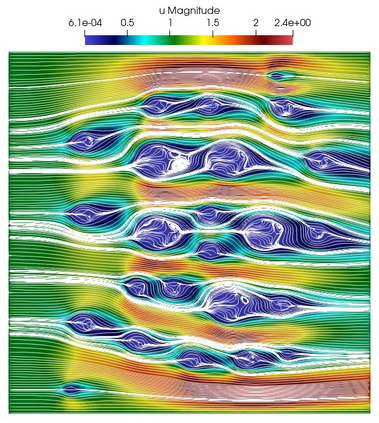
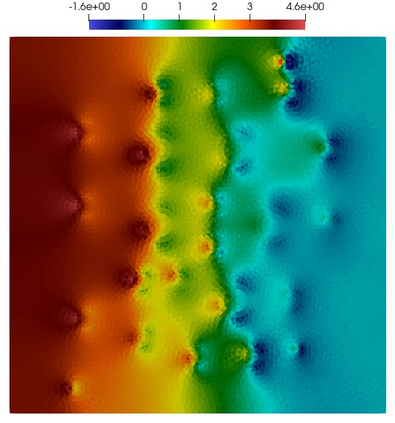
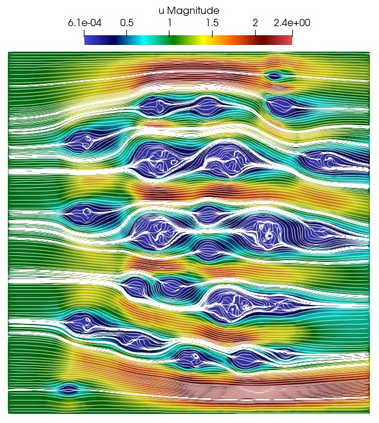
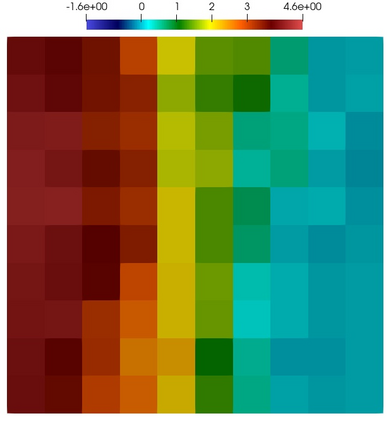
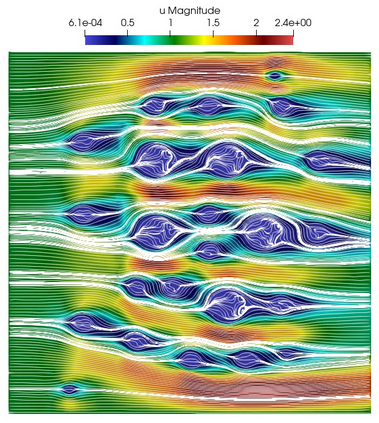
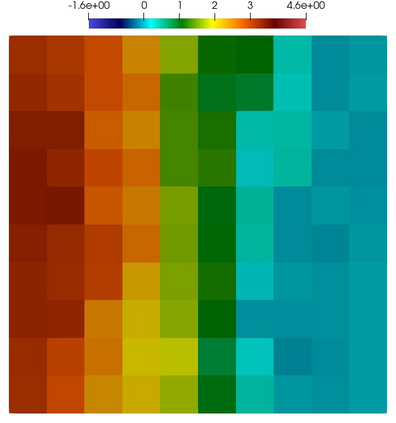
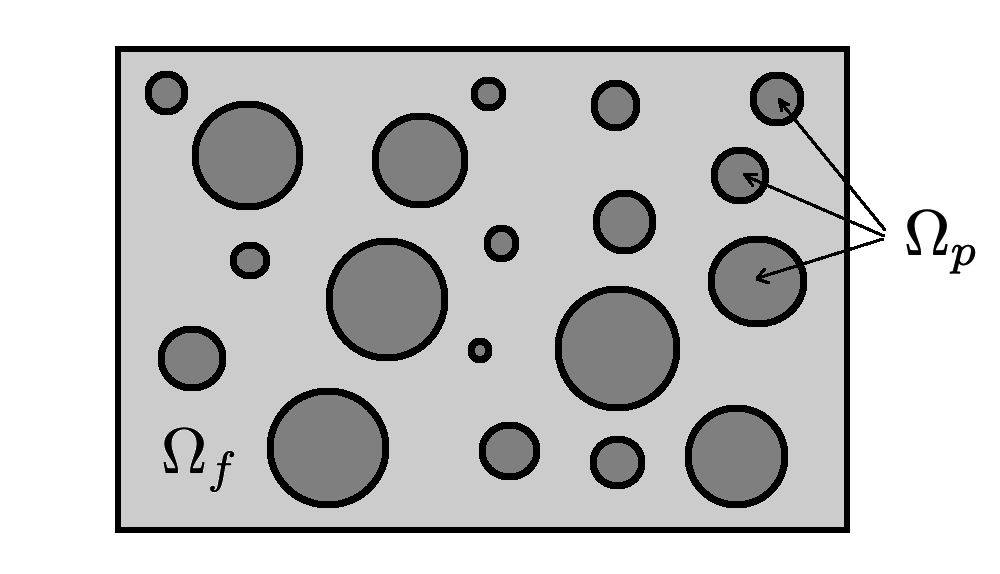
Numerical treatment of the problem of two-dimensional viscous fluid flow in and around circular porous inclusions is considered. The mathematical model is described by Navier-Stokes equation in the free flow domain $\Omega_f$ and nonlinear convective Darcy-Brinkman-Forchheimer equations in porous subdomains $\Omega_p$. It is well-known that numerical solutions of the problems in such heterogeneous domains require a very fine computational mesh that resolve inclusions on the grid level. The size alteration of the relevant system requires model reduction techniques. Here, we present a multiscale model reduction technique based on the Generalized Multiscale Finite Element Method (GMsFEM). We discuss construction of the multiscale basis functions for the velocity fields based on the solution of the local problems with and without oversampling strategy. Three test cases are considered for a given choice of the three key model parameters, namely, the Reynolds number ($Re$), the Forchheimer coefficient ($C$) and the Darcy number ($Da$). For the test runs, the Reynolds number values are taken to be $Re = 1, 10, 100$ while the Forchheimer coefficient and Darcy number are chosen as $C= 1, 10$ and $Da = 10^{-5}, 10^{-4}, 10^{-3}$, respectively. We numerically study the convergence of the method as we increase the number of multiscale basis functions in each domain, and observe good performance of the multiscale method.
翻译:数学模型由Navier-Stokes 等式描述,在自由流域$\ Omega_f$f$ 和非线性对流式 Darcy-Brinkman-Forchheimer 等式中,以松散的子域为单位, $\ Omega_p$。 众所周知, 解决这些杂交域的问题的数字方案需要非常精细的计算网格级网格的网格, 相关系统的规模改变需要模型减少技术。 在这里, 我们展示了基于通用多级硬化元素法( GMSFEM) 的多级模型减少技术。 我们讨论根据本地问题的解决办法和不过分标注策略来构建速度场的多级基函数。 对于三种关键模型参数的某个特定选择, 即Remonz 数( Re$ $)、 Forchheimer 系数( Formall) $1, 我们所选择的10- damal 标准值为10美元。