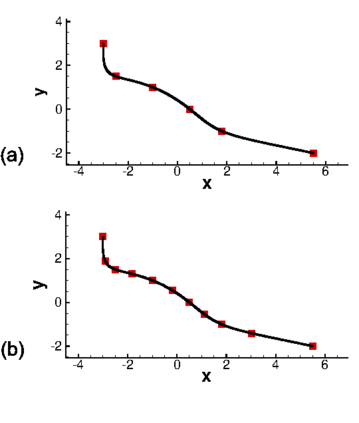
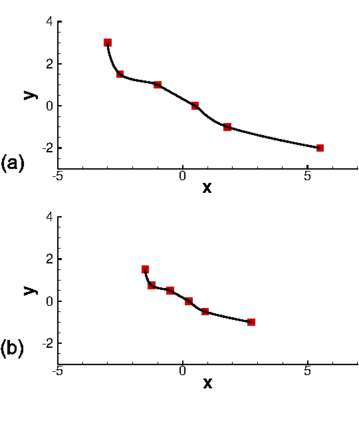
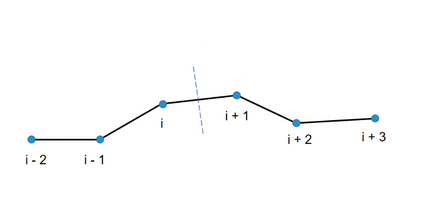
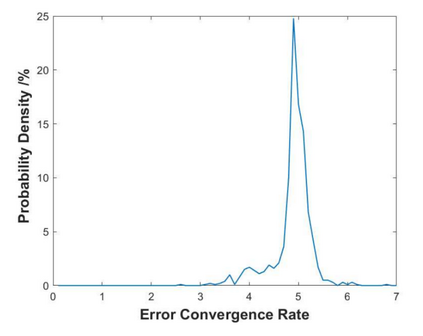
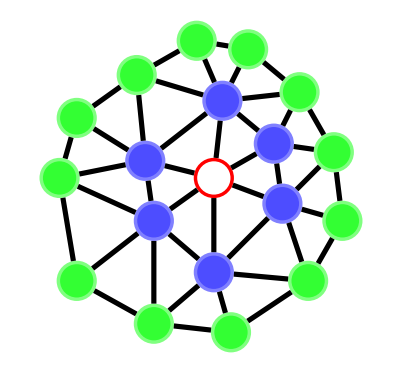
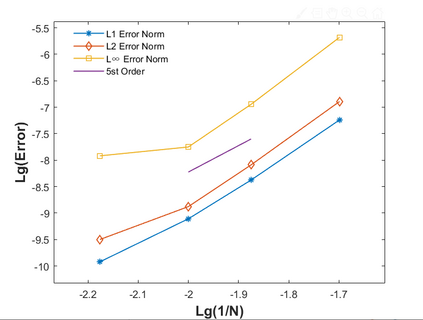
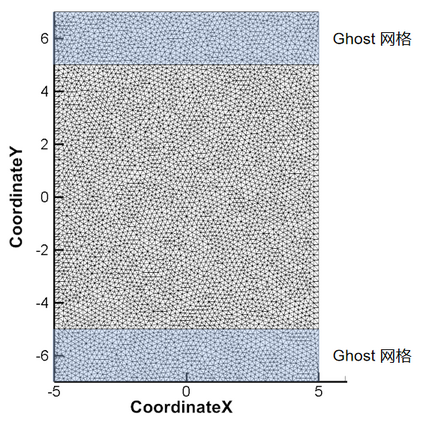
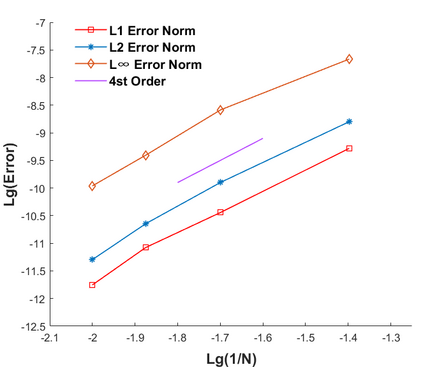
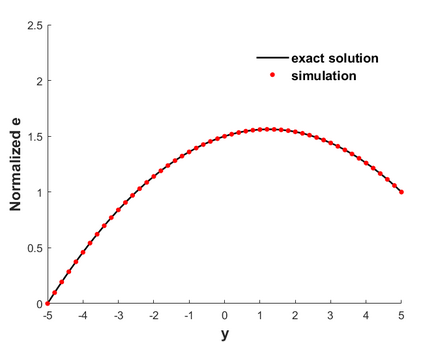
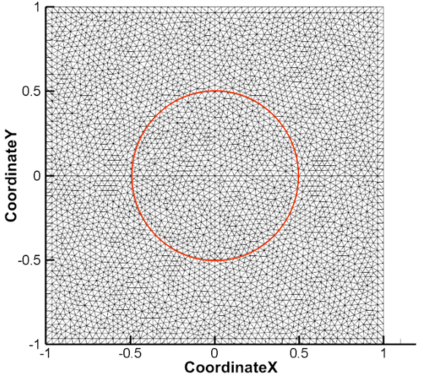
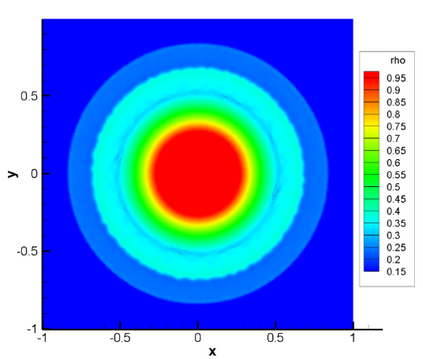
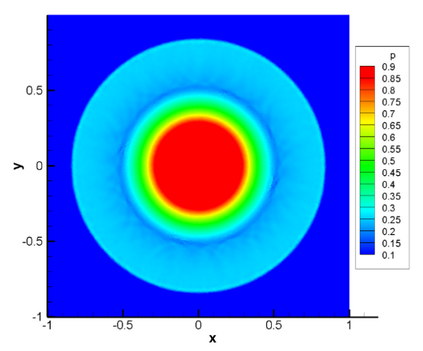
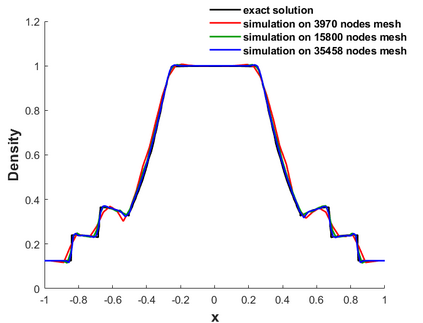
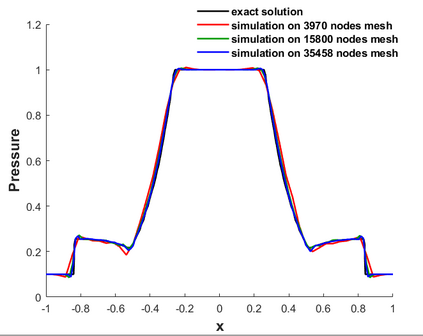
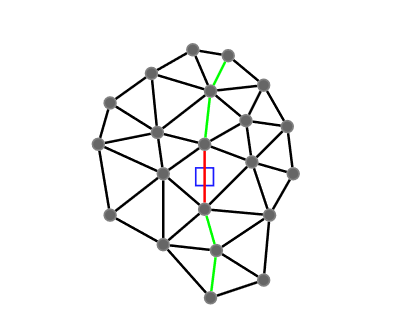
A high order finite difference method is proposed for unstructured meshes to simulate compressible inviscid/viscous flows with/without discontinuities. In this method, based on the strong form equation, the divergence of the flux on each vertex is computed directly from fluxes nearby by means of high order least-square. In order to capture discontinuities, numerical flux of high order accuracy is calculated on each edge and serves as supporting data of the least-square computation of the divergence. The high accuracy of the numerical flux depends on the high order WENO interpolation on each edge. To reduce the computing cost and complexity, a curvlinear stencil is assembled for each edge so that the economical one-dimensional WENO interpolation can be applied. With the derivatives introduced, two-dimensional Hermite interpolation on a curvilinear stencil is applied to keep the stencil compact and avoids using many supporting points. In smooth region, the Hermite least-square 2D interpolation of 5 nodes is adopted directly to achieve the fifth order accuracy. Near a discontinuity, three values obtained by means of least-square 2D interpolation of 3 nodes, are weighted to obtain one value of the second order accuracy. After obtaining the flow states on both sides of the middle point of an edge, numerical flux of high order accuracy along the edge can be calculated. For inviscid flux, analytical flux on vertices and numerical flux along edges are used to compute the divergence. While for viscous flux, only analytical viscous flux on vertices are used. The divergence of the fluxes and their derivatives on each vertex are used to update the conservative variables and their derivatives with an explicit Runger-Kutta time scheme. Several canonical numerical cases were solved to test the accuracy and the capability of shock capturing of this method.
翻译:对于不结构化的介质,建议一种高顺序定值差异法,以模拟不连续/不连续的不固定的折叠式内流。在这个方法中,根据强烈的形式方程式,每个顶端的通量差异直接从附近的通量中计算。为了捕捉不连续,在每个边缘计算出高顺序精确度的数字通量,作为计算差分最低方位计算的数据支持数据。数字通量的高度精确度取决于每个边缘的易变异度(WENO)内插。为了降低计算成本和复杂性,每个边缘都组装了曲线内分值,这样可以应用经济的单维端的WENO内插值。随着衍生物的引入,在二次曲线上计算出高顺序的Hermite内插值,从而避免使用许多支持点。在平滑度区域,赫米特最低端的2D内替值在5节点上调高顺序。为了降低计算成本,在5节点上直接采用曲线内置值的曲线递增速度递增速度, 接近1级的直径直径直值,使用三种计算法方法,在直径直径直到直至直径的货币内置的变值。