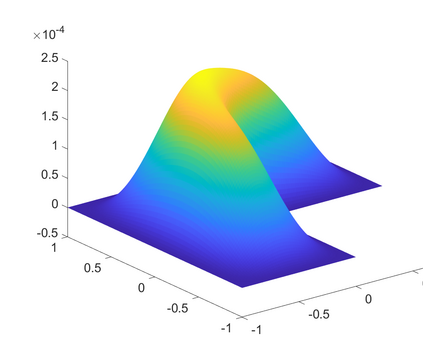
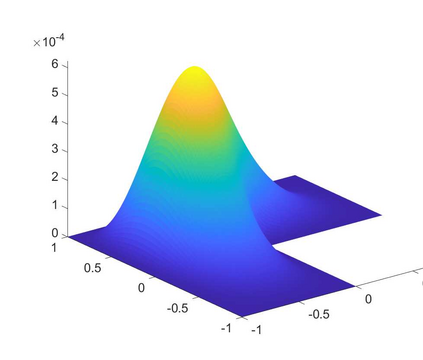
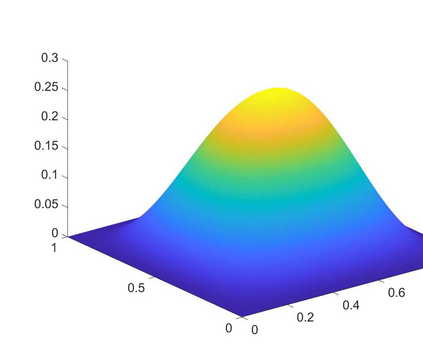
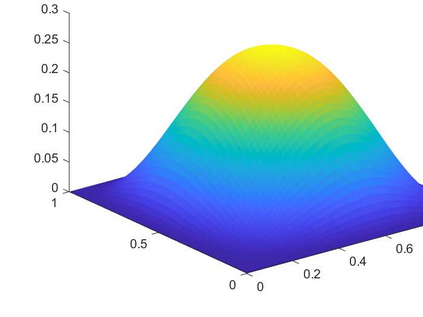
This paper deals with the numerical approximation of the biharmonic inverse source problem in an abstract setting in which the measurement data is finite-dimensional. This unified framework in particular covers the conforming and nonconforming finite element methods (FEMs). The inverse problem is analysed through the forward problem. Error estimate for the forward solution is derived in an abstract set-up that applies to conforming and Morley nonconforming FEMs. Since the inverse problem is ill-posed, Tikhonov regularisation is considered to obtain a stable approximate solution. Error estimate is established for the regularised solution for different regularisation schemes. Numerical results that confirm the theoretical results are also presented.
翻译:本文在测量数据为有限维度的抽象环境中处理双调反源问题的数字近似值。 这个统一框架特别涵盖符合和不符合符合的有限元素方法(FEMS) 。 反向问题通过前期问题分析。 前方解决方案的误差估计是在适用于符合和Morley不符合FEMs的抽象设置中得出的。 由于反向问题存在错误, Tikhonoov 常规化被认为是一个稳定的近似解决方案。 为不同常规化方案定出错误估计值。 也提供了证实理论结果的数值结果。