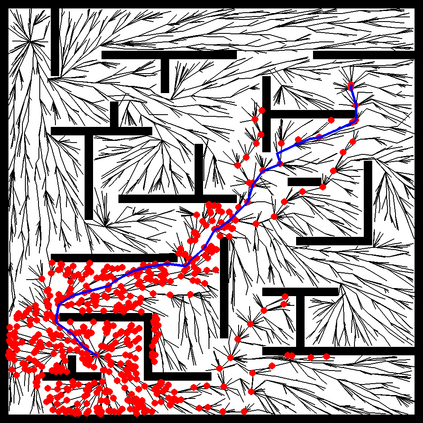
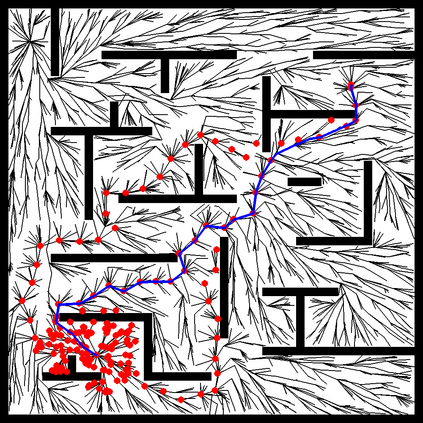
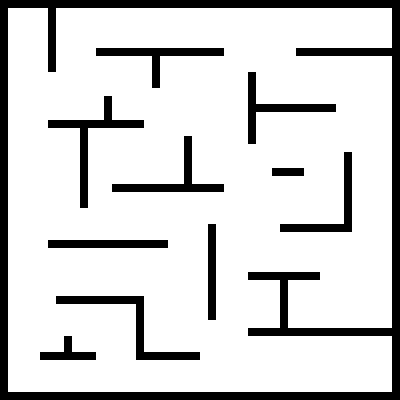
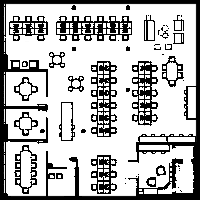
In this paper, we present a new algorithm that extends RRT* and RT-RRT* for online path planning in complex, dynamic environments. Sampling-based approaches often perform poorly in environments with narrow passages, a feature common to many indoor applications of mobile robots as well as computer games. Our method extends RRT-based sampling methods to enable the use of an assisting distance metric to improve performance in environments with obstacles. This assisting metric, which can be any metric that has better properties than the Euclidean metric when line of sight is blocked, is used in combination with the standard Euclidean metric in such a way that the algorithm can reap benefits from the assisting metric while maintaining the desirable properties of previous RRT variants - namely probabilistic completeness in tree coverage and asymptotic optimality in path length. We also introduce a new method of targeted rewiring, aimed at shortening search times and path lengths in tasks where the goal shifts repeatedly. We demonstrate that our method offers considerable improvements over existing multi-query planners such as RT-RRT* when using diffusion distance as an assisting metric; finding near-optimal paths with a decrease in search time of several orders of magnitude. Experimental results show planning times reduced by 99.5% and path lengths by 9.8% over existing real-time RRT planners in a variety of environments.
翻译:在本文中,我们提出了一个新的算法,在复杂、动态的环境中扩展RRT* 和RT-RRT* 进行在线路径规划。基于抽样的方法往往在狭小通道的环境中表现不佳,这是移动机器人和计算机游戏许多室内应用的共同特点。我们的方法扩展了基于RRT的抽样方法,以便能够使用协助的距离测量方法来改善有障碍环境中的性能。这种协助性指标可以是任何在视线阻塞时比Euclidean 度量值更好的指标,它与标准的Euclidean 度量值结合使用,使该算法能够从协助度值中获益,同时保持先前RRT变量的可取性(即树木覆盖的概率完整性和路径长度的微调优化性)。我们还采用了一种新的定向重新定位方法,旨在缩短目标反复移动时段的搜索时间和路径长度。我们证明,我们的方法比RT-RRT* 等现有多管规划者在使用扩散距离作为衡量标准时可以大大改进,从而能够从援助度中受益,同时保持先前RMT的参数,同时保持先前RRT变量值,同时保持以前的RRT变量的可取性特性,同时维持以前的RRT变量的特性,同时在协助度值,同时,并保持先前RRT的准值,同时在树覆盖率的准度的准度的准度的准度的准度的准度的准度的准度的准度的准度的准度的准度;通过近9:通过实验度的准度规划,以缩小了近9:在精确度的准度为10度的实验度,通过实验度为缩短时间段距度,以缩小了近9:通过实验度,通过实验度为10度,通过实验度为10度的准度,以缩小了近9度,以实验性速度为10度的准度,通过实验度为10度为10度为10度为10度,通过实验性速度为10度,通过实验度,以缩小了近9度,以缩小,以缩小,以实验性速度为10度为10度为10度。