An Upwind Generalized Finite Difference Method for Meshless Solution of Two-phase Porous Flow Equations

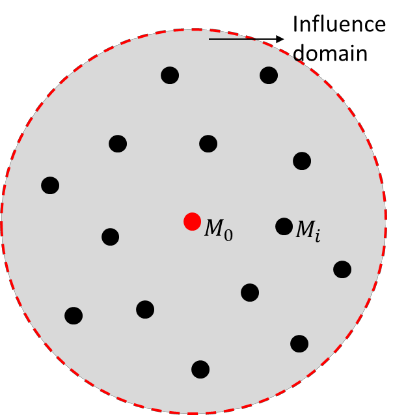
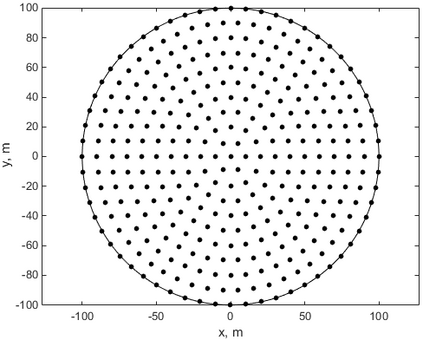
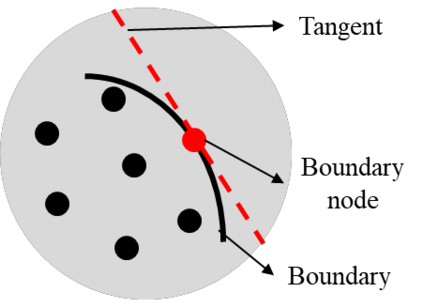
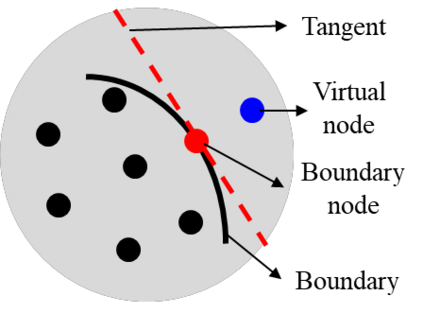
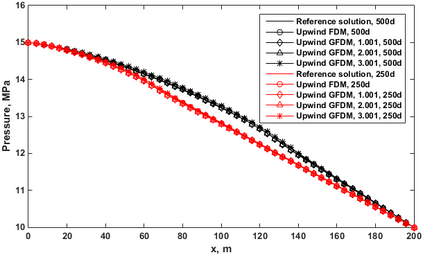
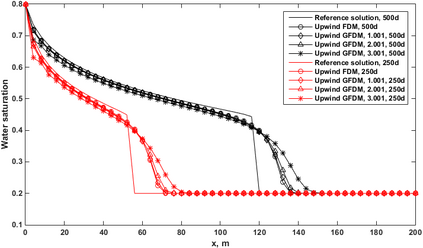
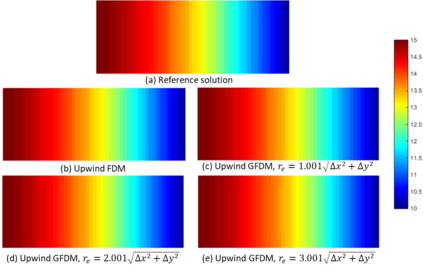
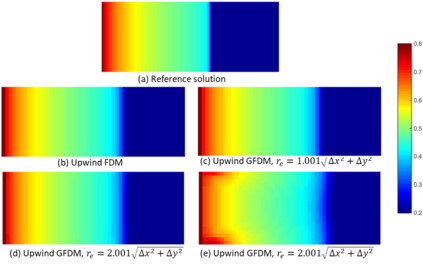
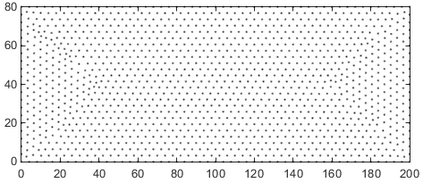
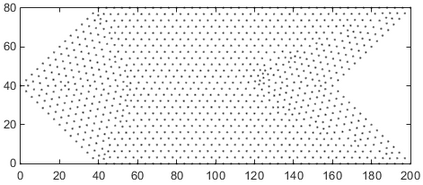
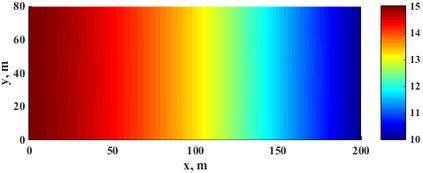
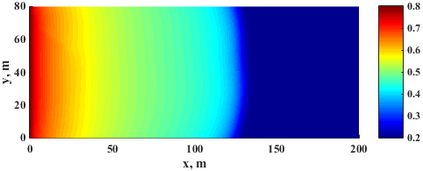
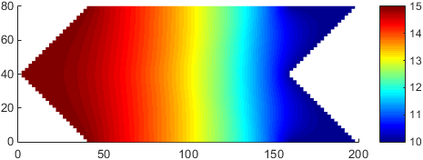
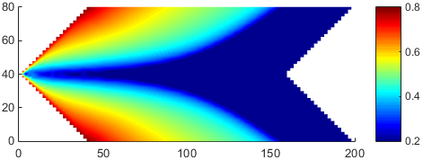
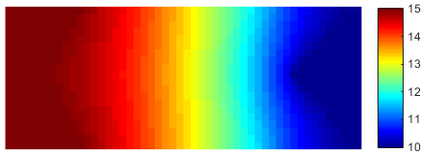
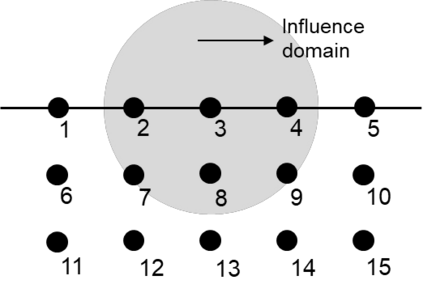
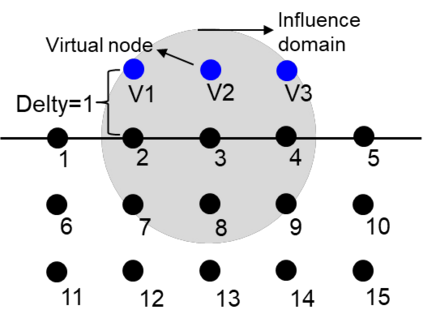
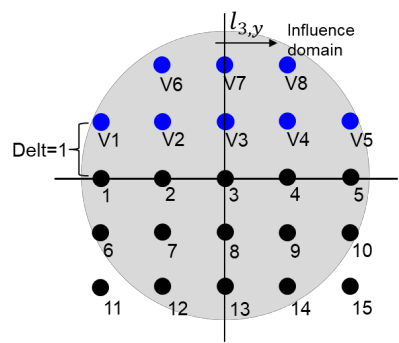
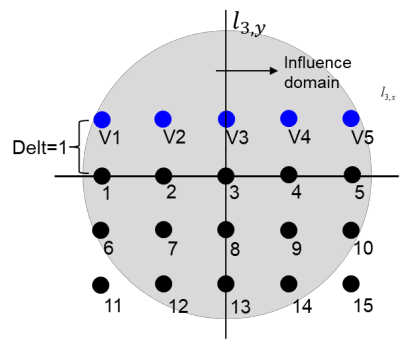
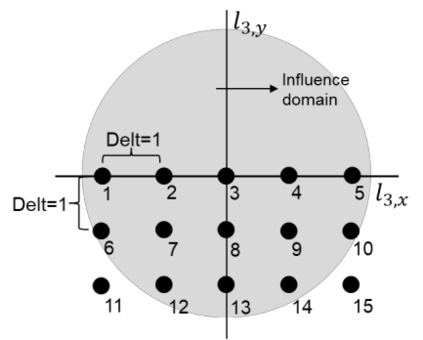
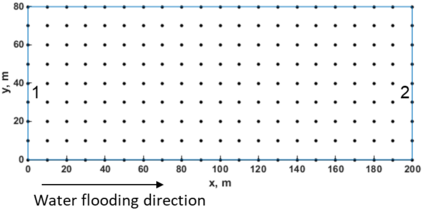
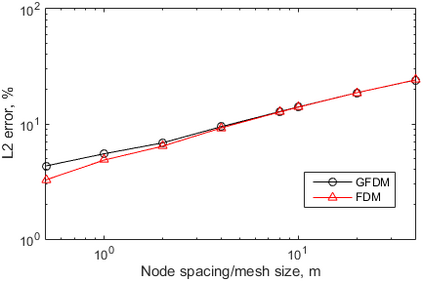
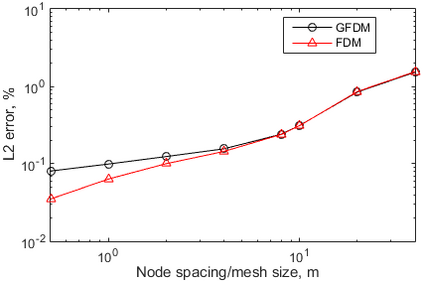
This paper makes the first attempt to apply newly developed upwind GFDM for the meshless solution of two-phase porous flow equations. In the presented method, node cloud is used to flexibly discretize the computational domain, instead of complicated mesh generation. Combining with moving least square approximation and local Taylor expansion, spatial derivatives of oil-phase pressure at a node are approximated by generalized difference operators in the local influence domain of the node. By introducing the first-order upwind scheme of phase relative permeability, and combining the discrete boundary conditions, fully-implicit GFDM-based nonlinear discrete equations of the immiscible two-phase porous flow are obtained and solved by the nonlinear solver based on the Newton iteration method with the automatic differentiation, to avoid the additional computational cost and possible computational instability caused by sequentially coupled scheme. Two numerical examples are implemented to test the computational performances of the presented method. Detailed error analysis finds the two sources of the calculation error, roughly studies the convergence order, and points out the significant effect of the symmetry or uniformity of the node allocation in the node influence domain on the accuracy of generalized difference operators, and the radius of the node influence domain should be small to achieve high calculation accuracy, which is a significant difference between the studied parabolic two-phase porous flow problem and the elliptic problems when GFDM is applied. In all, the upwind GFDM with the fully implicit nonlinear solver and related analysis about computational performances given in this work may provide a critical reference for developing a general-purpose meshless numerical simulator for porous flow problems.