Fork or Fail: Cycle-Consistent Training with Many-to-One Mappings

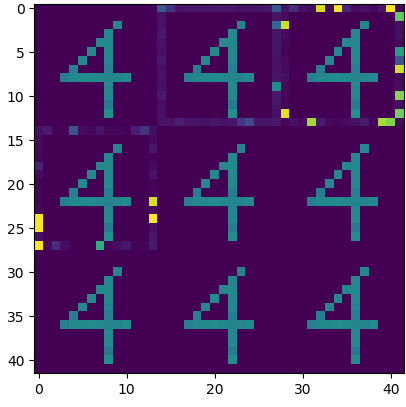
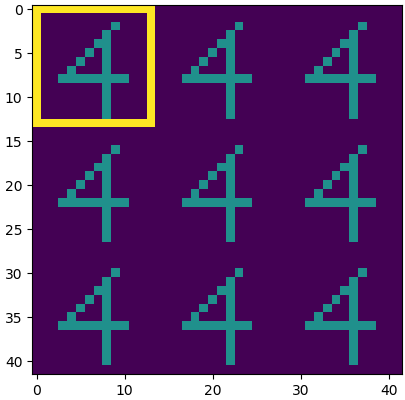
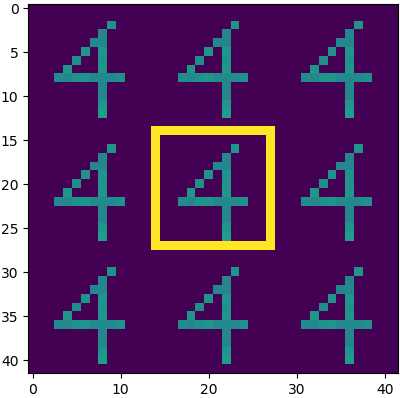
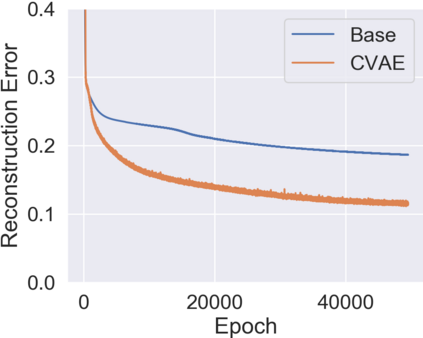
Cycle-consistent training is widely used for jointly learning a forward and inverse mapping between two domains of interest without the cumbersome requirement of collecting matched pairs within each domain. In this regard, the implicit assumption is that there exists (at least approximately) a ground-truth bijection such that a given input from either domain can be accurately reconstructed from successive application of the respective mappings. But in many applications no such bijection can be expected to exist and large reconstruction errors can compromise the success of cycle-consistent training. As one important instance of this limitation, we consider practically-relevant situations where there exists a many-to-one or surjective mapping between domains. To address this regime, we develop a conditional variational autoencoder (CVAE) approach that can be viewed as converting surjective mappings to implicit bijections whereby reconstruction errors in both directions can be minimized, and as a natural byproduct, realistic output diversity can be obtained in the one-to-many direction. As theoretical motivation, we analyze a simplified scenario whereby minima of the proposed CVAE-based energy function align with the recovery of ground-truth surjective mappings. On the empirical side, we consider a synthetic image dataset with known ground-truth, as well as a real-world application involving natural language generation from knowledge graphs and vice versa, a prototypical surjective case. For the latter, our CVAE pipeline can capture such many-to-one mappings during cycle training while promoting textural diversity for graph-to-text tasks. Our code is available at github.com/QipengGuo/CycleGT