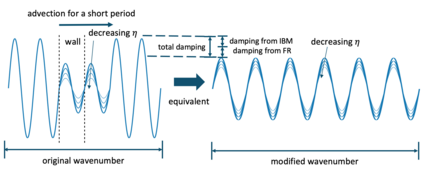
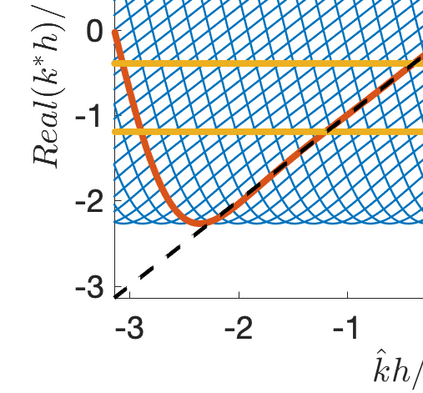
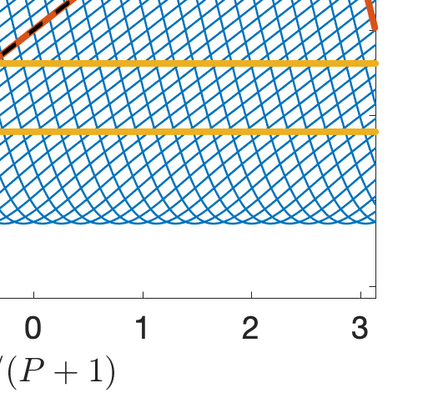
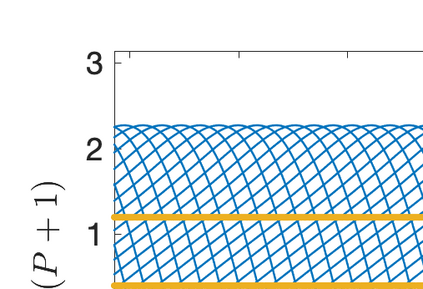
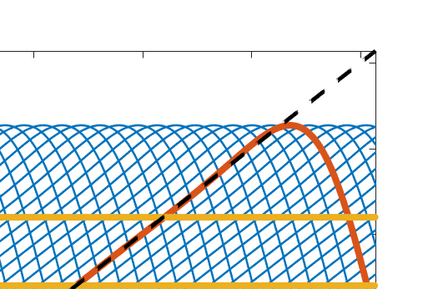
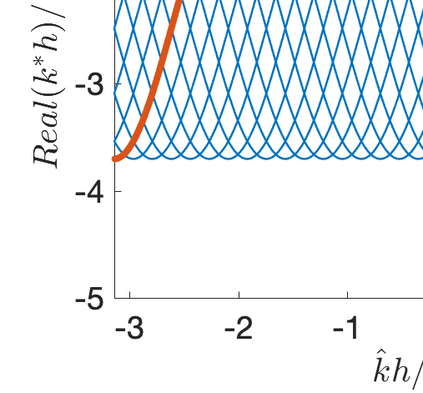
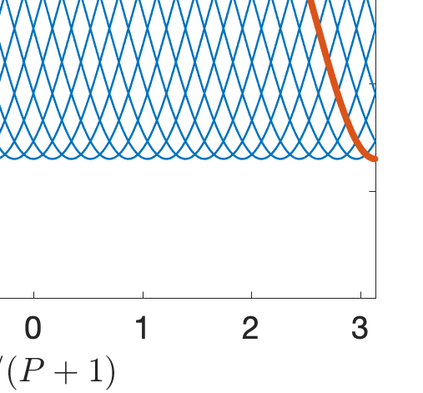
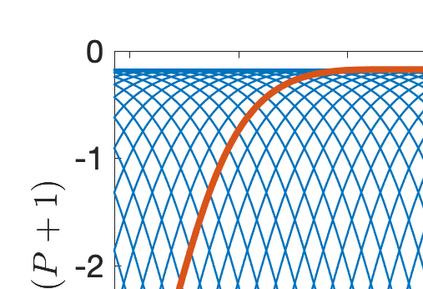
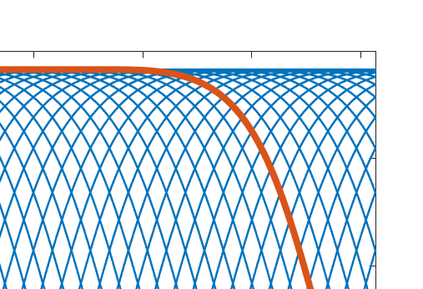
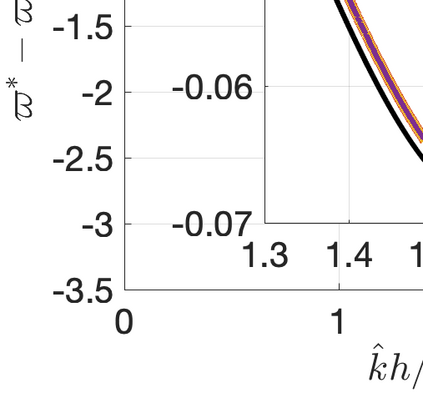
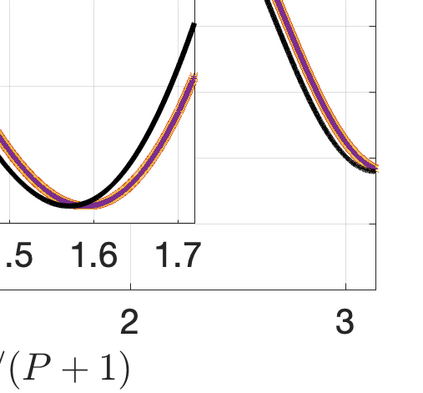
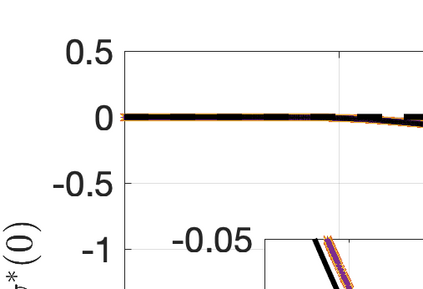
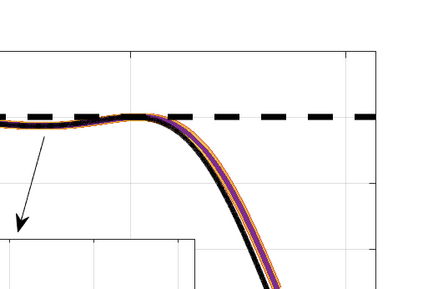
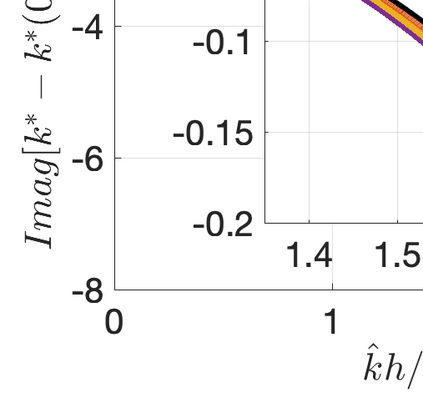
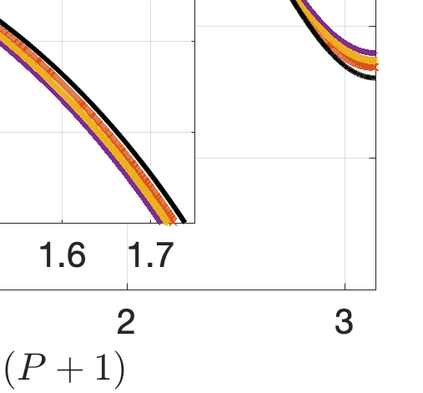
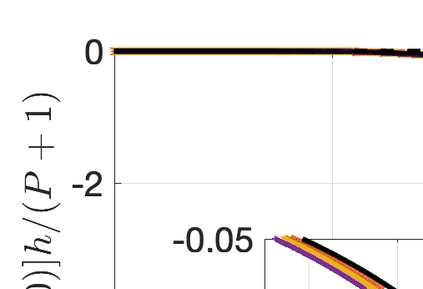
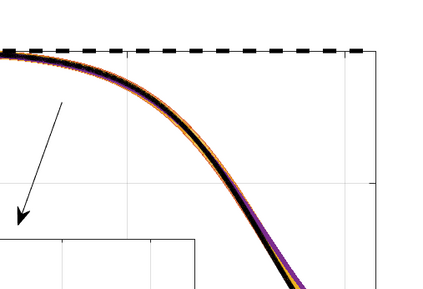
This paper presents eigensolution and non-modal analyses for immersed boundary methods (IBMs) based on volume penalization for the linear advection equation. This approach is used to analyze the behavior of flux reconstruction (FR) discretization, including the influence of polynomial order and penalization parameter on numerical errors and stability. Through a semi-discrete analysis, we find that the inclusion of IBM adds additional dissipation without changing significantly the dispersion of the original numerical discretization. This agrees with the physical intuition that in this type of approach, the solid wall is modelled as a porous medium with vanishing viscosity. From a stability point view, the selection of penalty parameter can be analyzed based on a fully-discrete analysis, which leads to practical guidelines on the selection of penalization parameter. Numerical experiments indicate that the penalization term needs to be increased to damp oscillations inside the solid (i.e. porous region), which leads to undesirable time step restrictions. As an alternative, we propose to include a second-order term in the solid for the no-slip wall boundary condition. Results show that by adding a second-order term we improve the overall accuracy with relaxed time step restriction. This indicates that the optimal value of the penalization parameter and the second-order damping can be carefully chosen to obtain a more accurate scheme. Finally, the approximated relationship between these two parameters is obtained and used as a guideline to select the optimum penalty terms in a Navier-Stokes solver, to simulate flow past a cylinder.
翻译:本文根据对线性对冲方程式的体积处罚,对沉浸的边界方法(IBMs)进行解析和非模式分析。 这种方法用于分析通量重建( FR) 分解的行为, 包括多式秩序和惩罚参数对数值错误和稳定性的影响。 通过半分化分析, 我们发现, 将IBM 纳入会增加更多的分解, 而不会显著改变原始数字分解的分散性。 这与物理直觉相一致, 在这种方法中, 固态墙是仿制成一个有渗漏的介质, 其模范是, 固态墙的模范是, 从稳定点的角度, 选择惩罚参数的选择可以基于完全分解的分解( FR) 分析( FR), 从而得出关于选择惩罚参数的实用指南。 数值实验表明, 将惩罚术语加到固体( i.e. loby 区域) 内的振荡度, 这会导致不可取的时间步骤限制。 作为替代办法, 我们提议在不折时序整体边界规则中增加第二个固定的第二顺序, 和最精确的精确度规则 。