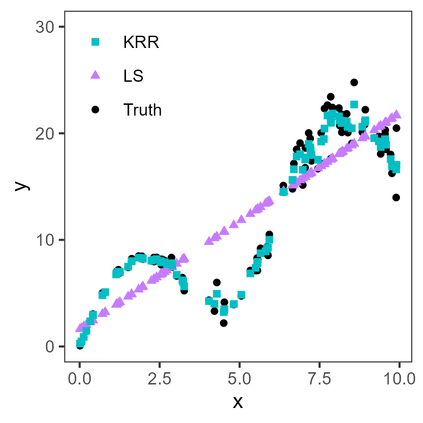
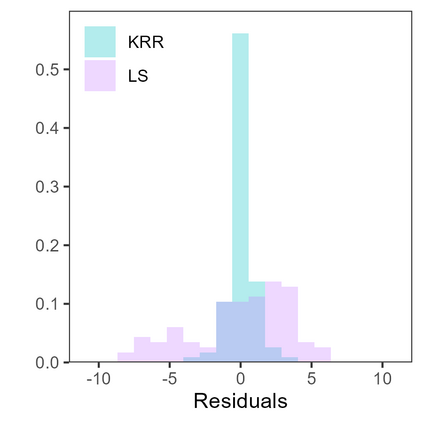
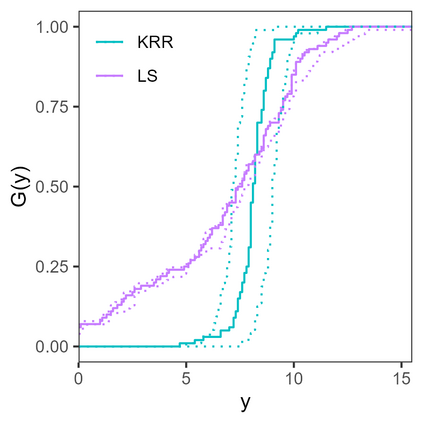
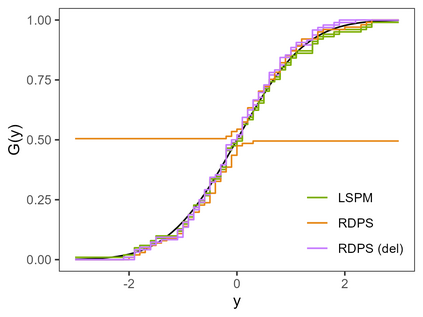
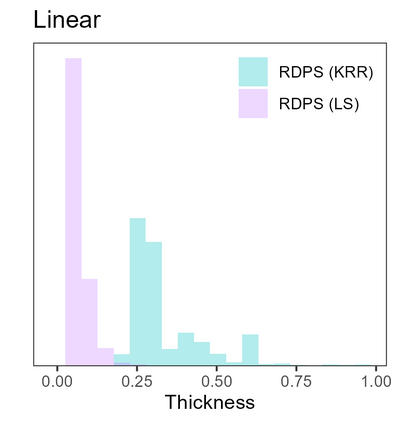
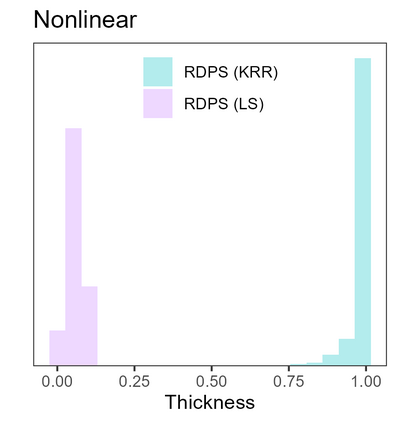
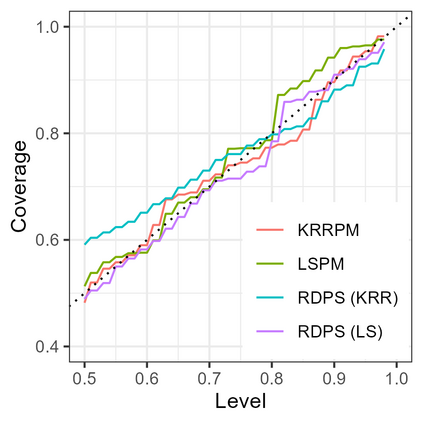
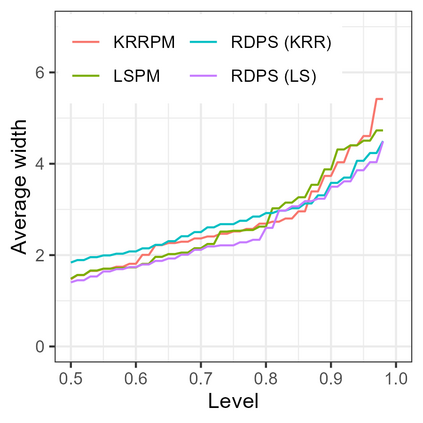
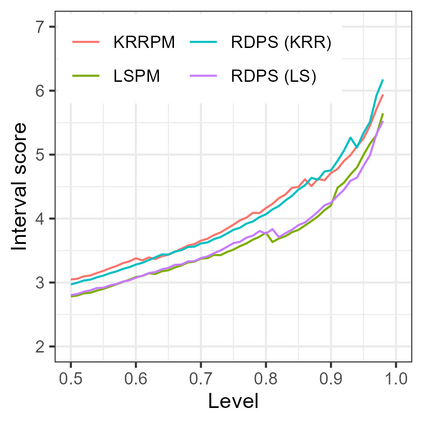
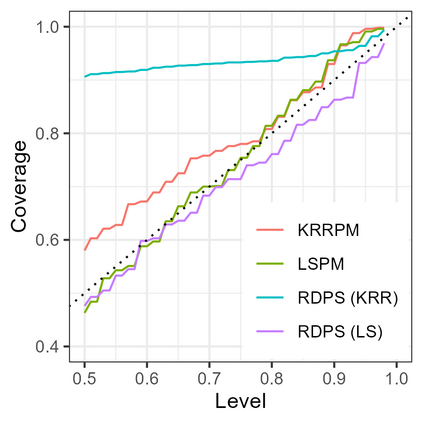
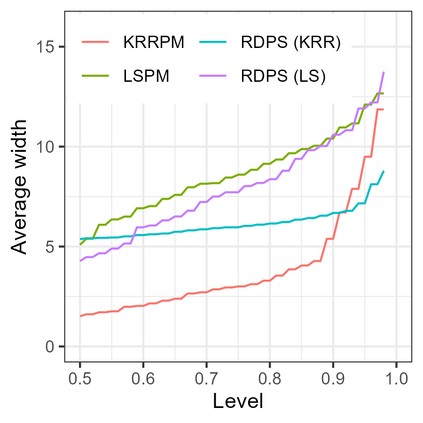
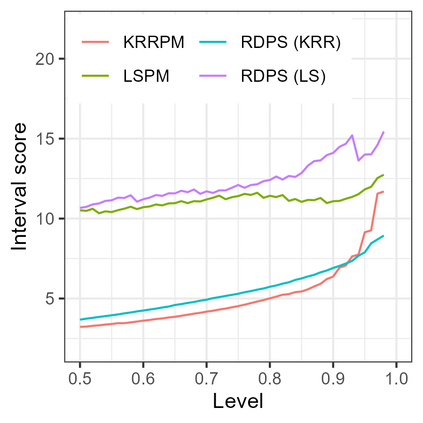
Conformal predictive systems are sets of predictive distributions with theoretical out-of-sample calibration guarantees. The calibration guarantees are typically that the set of predictions contains a forecast distribution whose prediction intervals exhibit the correct marginal coverage at all levels. Conformal predictive systems are constructed using conformity measures that quantify how well possible outcomes conform with historical data. However, alternative methods have been proposed to construct predictive systems with more appealing theoretical properties. We study an approach to construct predictive systems that we term Residual Distribution Predictive Systems. In the split conformal setting, this approach nests conformal predictive systems with a popular class of conformity measures, providing an alternative perspective on the classical approach. In the full conformal setting, the two approaches differ, and the new approach has the advantage that it does not rely on a conformity measure satisfying fairly stringent requirements to ensure that the predictive system is well-defined; it can readily be implemented alongside any point-valued regression method to yield predictive systems with out-of-sample calibration guarantees. The empirical performance of this approach is assessed using simulated data, where it is found to perform competitively with conformal predictive systems. However, the new approach offers considerable scope for implementation with alternative regression methods.
翻译:暂无翻译