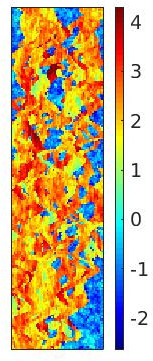
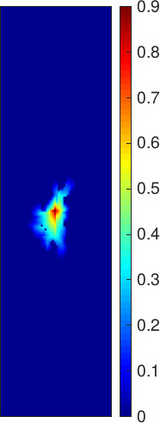
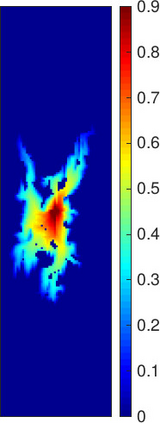
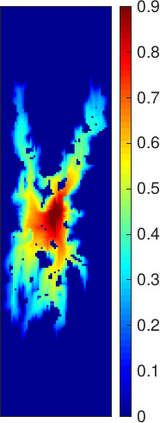
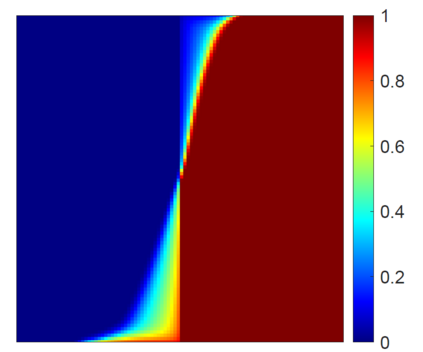
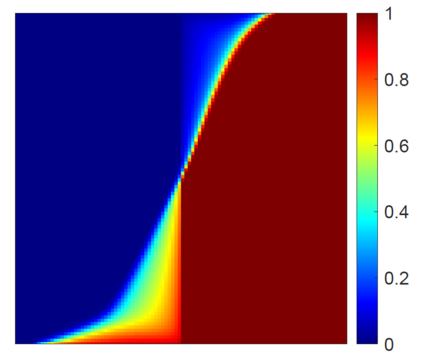
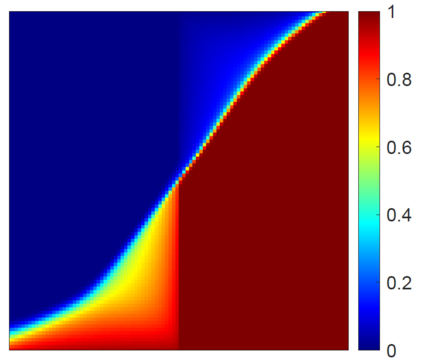
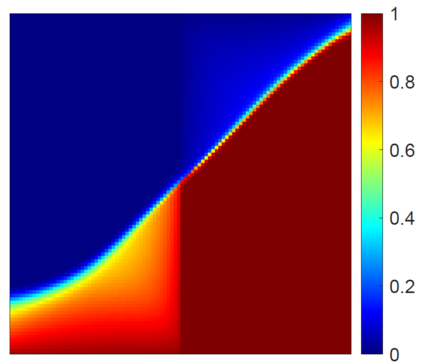
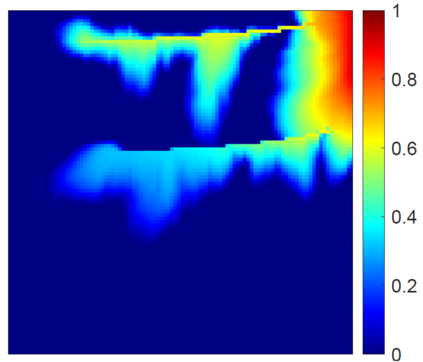
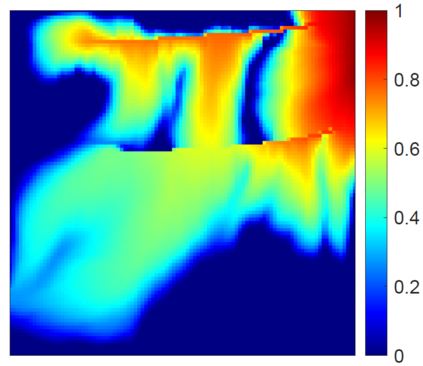
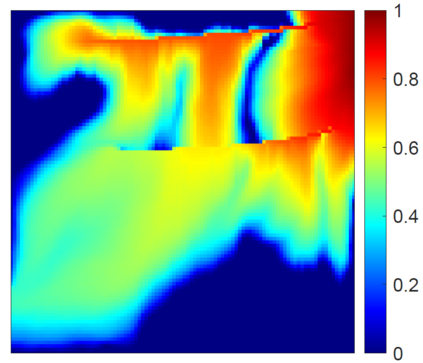
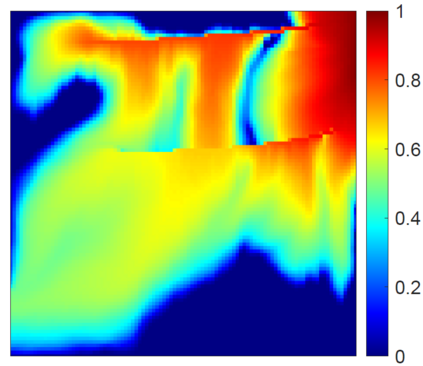
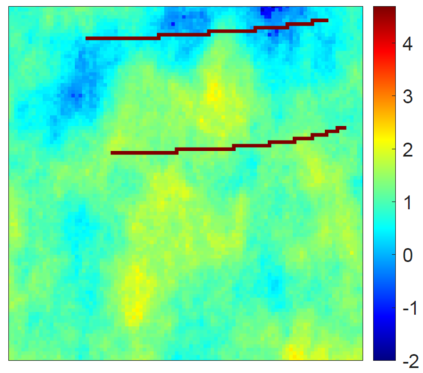
This work focuses on the development of a two-step field-split nonlinear preconditioner to accelerate the convergence of two-phase flow and transport in heterogeneous porous media. We propose a field-split algorithm named Field-Split Multiplicative Schwarz Newton (FSMSN), consisting in two steps: first, we apply a preconditioning step to update pressure and saturations nonlinearly by solving approximately two subproblems in a sequential fashion; then, we apply a global step relying on a Newton update obtained by linearizing the system at the preconditioned state. Using challenging test cases, FSMSN is compared to an existing field-split preconditioner, Multiplicative Schwarz Preconditioned for Inexact Newton (MSPIN), and to standard solution strategies such as the Sequential Fully Implicit (SFI) method or the Fully Implicit Method (FIM). The comparison highlights the impact of the upwinding scheme in the algorithmic performance of the preconditioners and the importance of the dynamic adaptation of the subproblem tolerance in the preconditioning step. Our results demonstrate that the two-step nonlinear preconditioning approach-and in particular, FSMSN-results in a faster outer-loop convergence than with the SFI and FIM methods. The impact of the preconditioners on computational performance-i.e., measured by wall-clock time-will be studied in a subsequent publication.
翻译:这项工作侧重于开发一个双步的外向非线性非线性先决条件,以加速分两阶段流动和多孔化介质运输的两阶段融合。我们提出一个名为FSMSN(FSMSN)的外向性算法,名为FSMSN(FSMSN),由两步组成:首先,我们采取一个先决条件步骤,通过按顺序解决大约两个子问题来更新压力和非线性讽刺;然后,我们采用一个全球步骤,依靠在先决条件状态下将系统线性化而获得的牛顿更新。利用具有挑战性的测试案例,FSMSSNSN将比照现有的外向性先决条件,即为不Exact Newton(MSPIN)预设的倍增性舒瓦兹,以及标准解决方案战略,如 " 完全隐含性(SFFFI)方法或完全隐性方法(FIM) " 等。比较突出表明,在先决条件步骤下,对FSMA-SM(FSM)的动态适应性能性调整方法的影响,在FSM(FSM)的后期性前期和后期性标准中,在FSIM(FSM-FSM-SM-SM-SM-SIM)的两步前期性、后期性标准方法中,其后期性、后期性、后期性能、后期性-SIM-SM-F-SIM-FSM-级性、后制方法中,对F-SL-SIM-SIM-SIM-后期性能、后期性与后制方法的影响将更快性-F-F-F-F-SM-F-SM-SM-F-F-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-F-S-S-S-S-SM-S-SIM-F-F-F-F-F-S-S-S-S-S-F-F-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-S-----S-S-S-