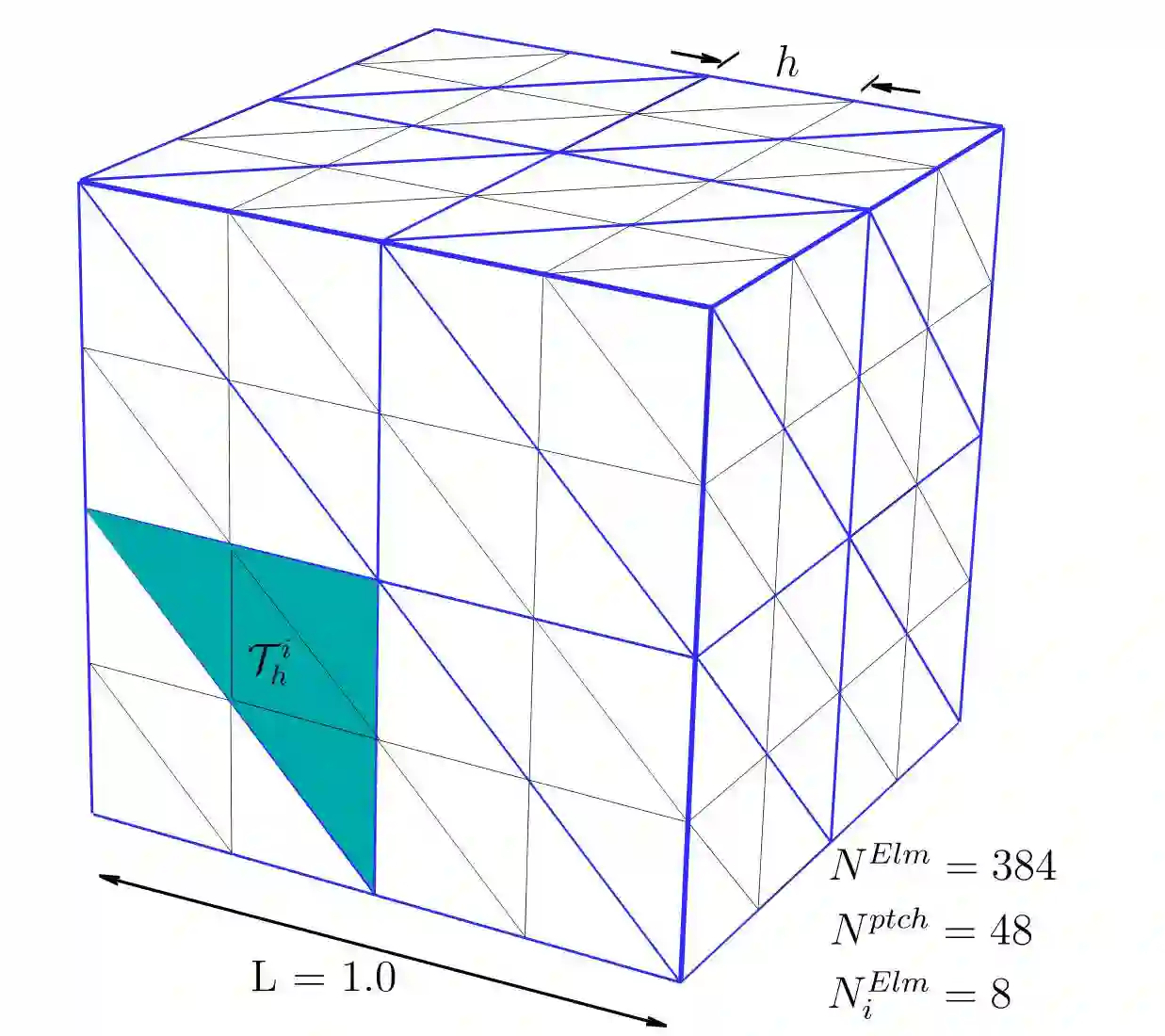
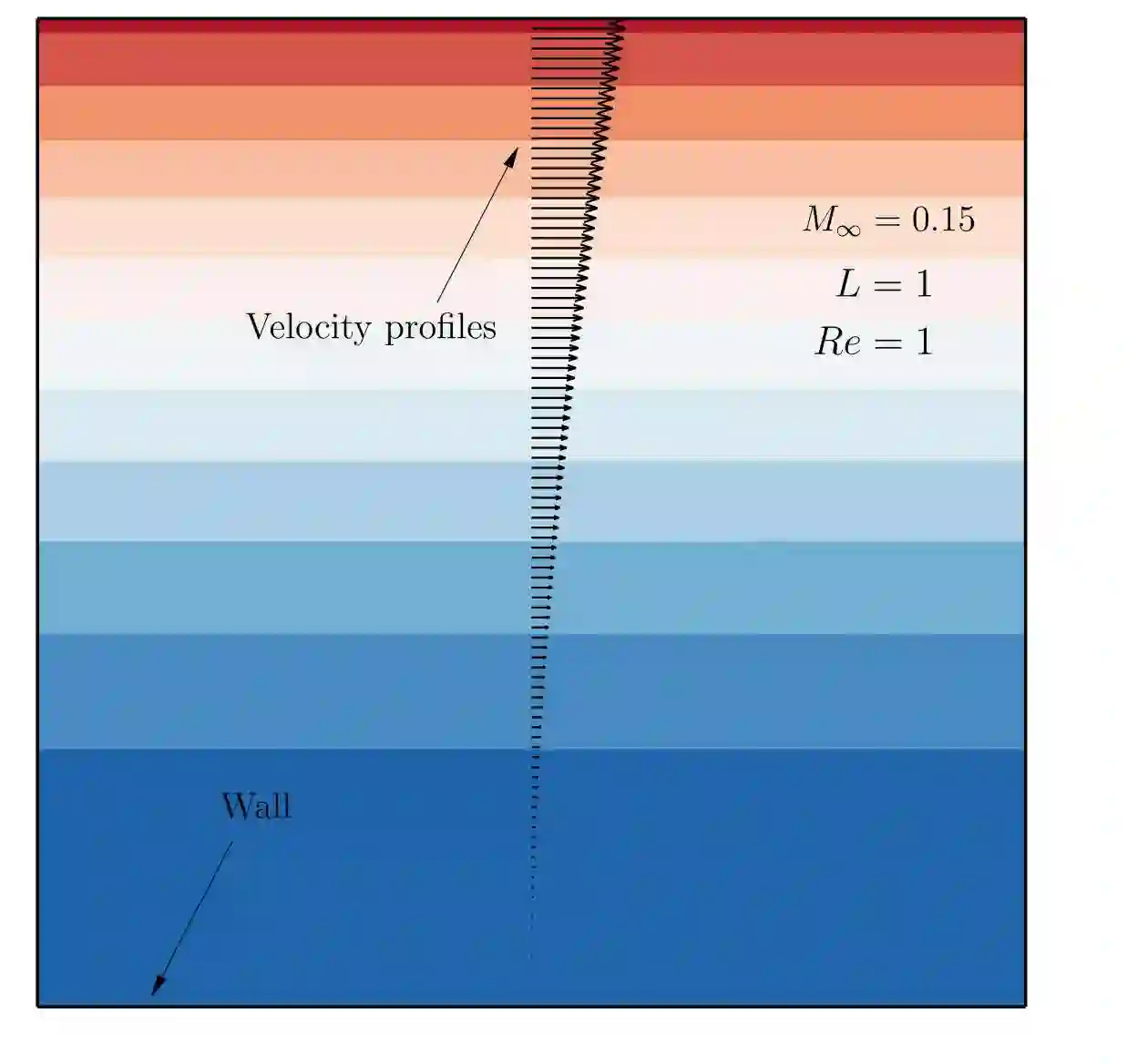
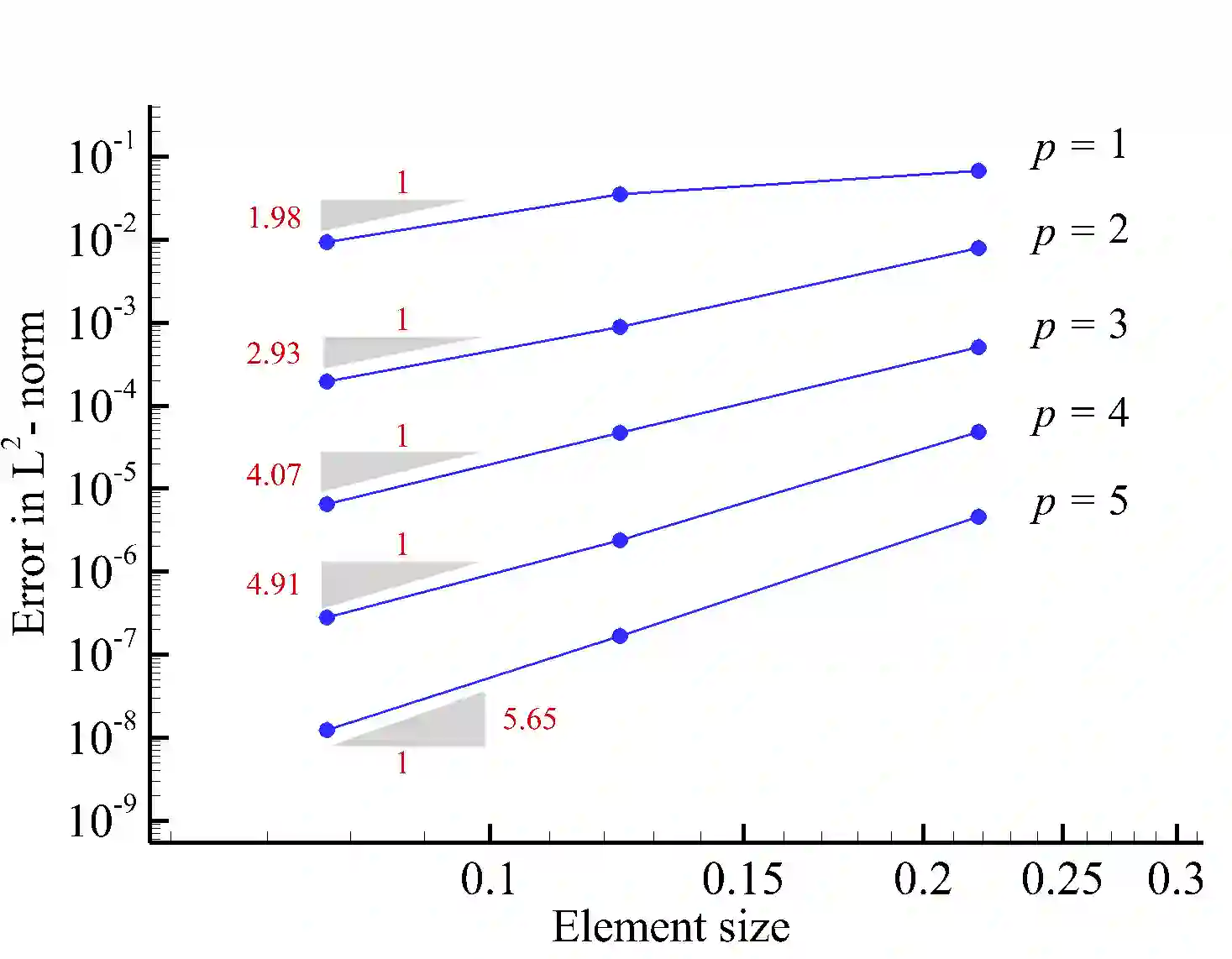
The macro-element variant of the hybridized discontinuous Galerkin (HDG) method combines advantages of continuous and discontinuous finite element discretization. In this paper, we investigate the performance of the macro-element HDG method for the analysis of compressible flow problems at moderate Reynolds numbers. To efficiently handle the corresponding large systems of equations, we explore several strategies at the solver level. On the one hand, we devise a second-layer static condensation approach that reduces the size of the local system matrix in each macro-element and hence the factorization time of the local solver. On the other hand, we employ a multi-level preconditioner based on the FGMRES solver for the global system that integrates well within a matrix-free implementation. In addition, we integrate a standard diagonally implicit Runge-Kutta scheme for time integration. We test the matrix-free macro-element HDG method for compressible flow benchmarks, including Couette flow, flow past a sphere, and the Taylor-Green vortex. Our results show that unlike standard HDG, the macro-element HDG method can operate efficiently for moderate polynomial degrees, as the local computational load can be flexibly increased via mesh refinement within a macro-element. Our results also show that due to the balance of local and global operations, the reduction in degrees of freedom, and the reduction of the global problem size and the number of iterations for its solution, the macro-element HDG method can be a competitive option for the analysis of compressible flow problems.
翻译:暂无翻译