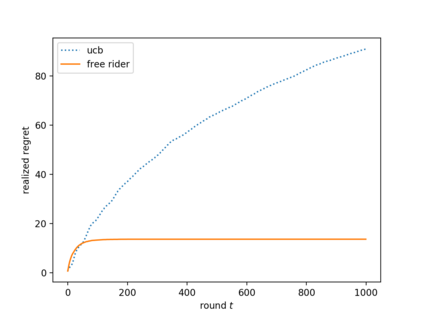
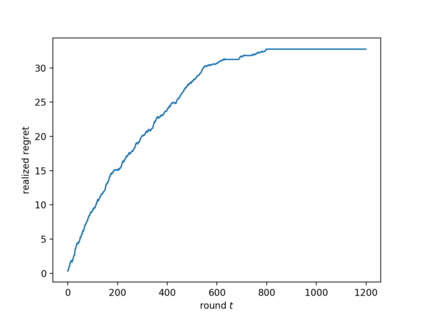
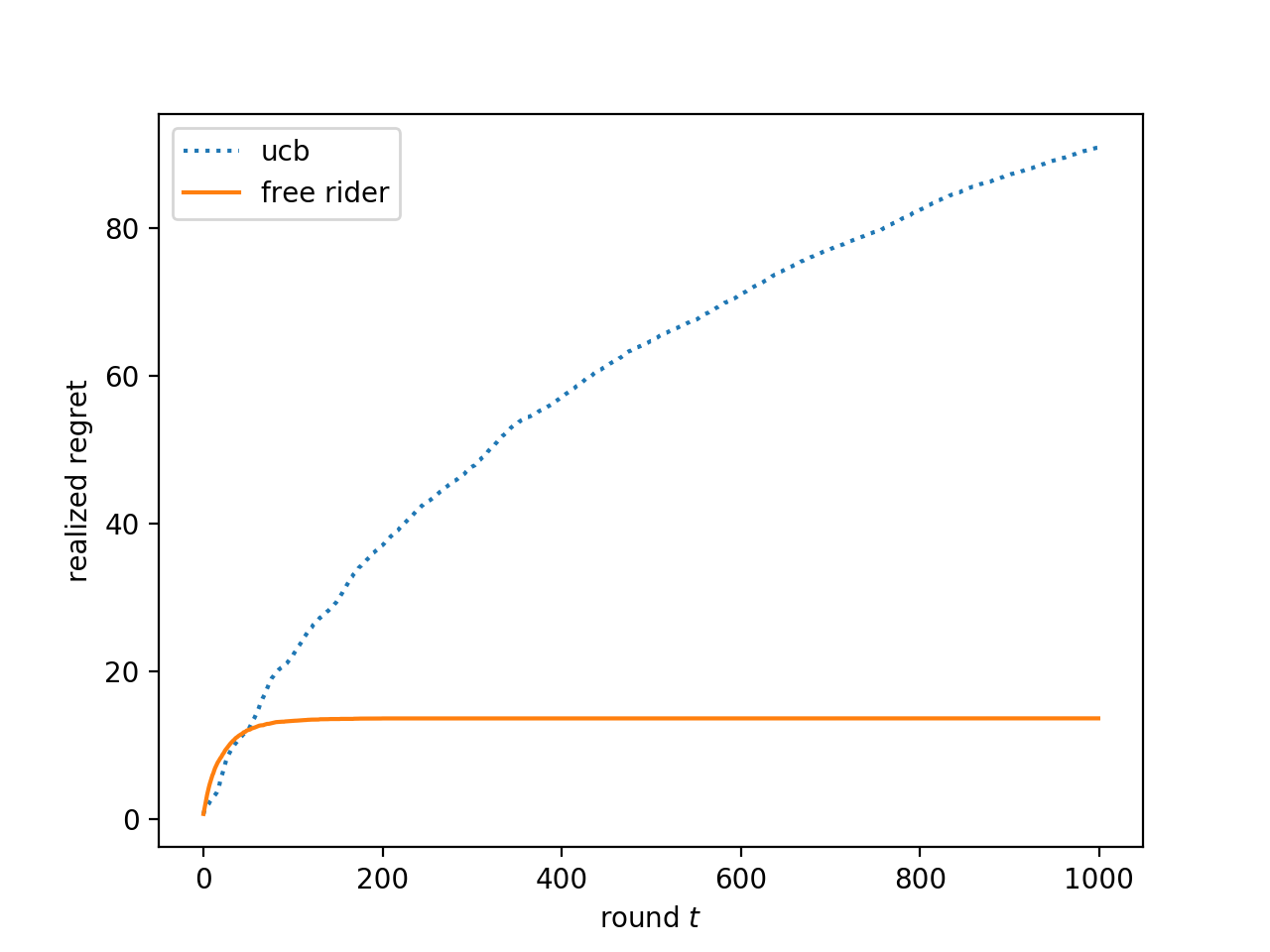
We consider the multi-armed bandit setting with a twist. Rather than having just one decision maker deciding which arm to pull in each round, we have $n$ different decision makers (agents). In the simple stochastic setting, we show that a "free-riding" agent observing another "self-reliant" agent can achieve just $O(1)$ regret, as opposed to the regret lower bound of $\Omega (\log t)$ when one decision maker is playing in isolation. This result holds whenever the self-reliant agent's strategy satisfies either one of two assumptions: (1) each arm is pulled at least $\gamma \ln t$ times in expectation for a constant $\gamma$ that we compute, or (2) the self-reliant agent achieves $o(t)$ realized regret with high probability. Both of these assumptions are satisfied by standard zero-regret algorithms. Under the second assumption, we further show that the free rider only needs to observe the number of times each arm is pulled by the self-reliant agent, and not the rewards realized. In the linear contextual setting, each arm has a distribution over parameter vectors, each agent has a context vector, and the reward realized when an agent pulls an arm is the inner product of that agent's context vector with a parameter vector sampled from the pulled arm's distribution. We show that the free rider can achieve $O(1)$ regret in this setting whenever the free rider's context is a small (in $L_2$-norm) linear combination of other agents' contexts and all other agents pull each arm $\Omega (\log t)$ times with high probability. Again, this condition on the self-reliant players is satisfied by standard zero-regret algorithms like UCB. We also prove a number of lower bounds.
翻译:我们以扭曲的方式看待多臂土匪的设置。 与其说只有一位决策人决定每轮拉动哪个臂, 不如说只有一位决策人来决定每轮拉动哪个臂, 我们拥有不同的决策者( 代理人) $ $ 。 在简单的随机设置中, 我们显示一个“ 免费搭乘” 代理商观察另一个“ 自力更生” 代理商能够只达到O(1)美元, 而当一个决策人孤立地玩耍的时候, 与一个低度的 美元相比, 我们只能以低度的 美元 。 这个结果是, 当一个自力更生的代理商至少拉动 $\ gamma = = 美元 。 在一个直线性背景中, 一个直线性代理商会拉动 $ 。