Is simplicity still possible for a more accurate approximation to the perimeter of the ellipse? or, Using the exponential function to further improve the second Ramanujan's approximation

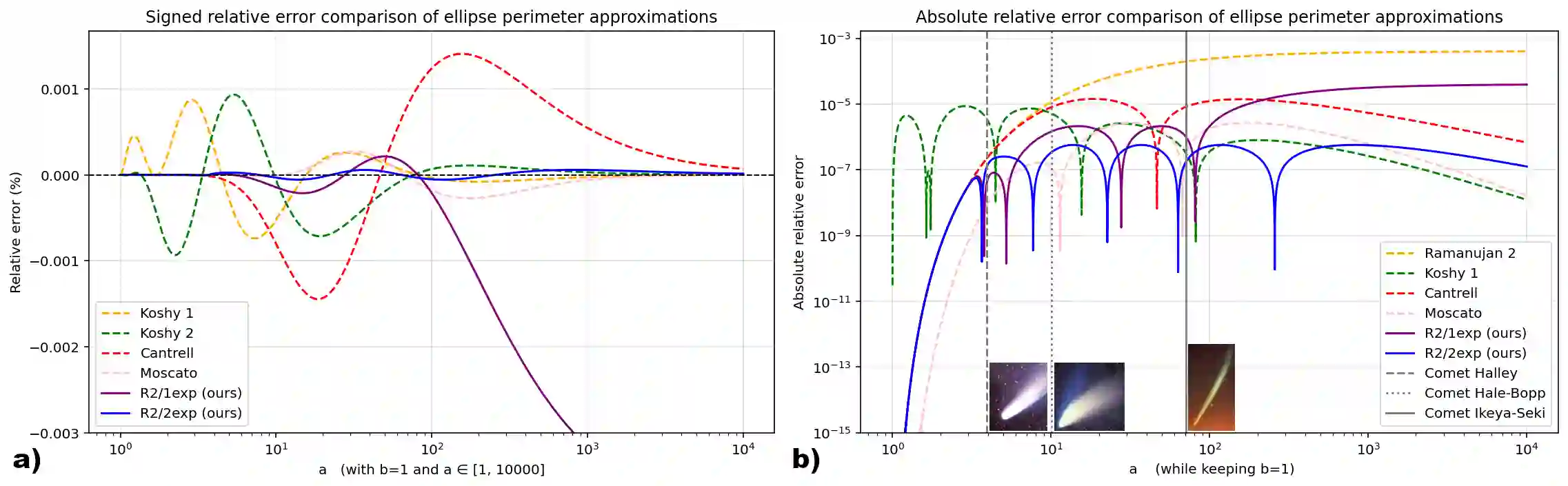
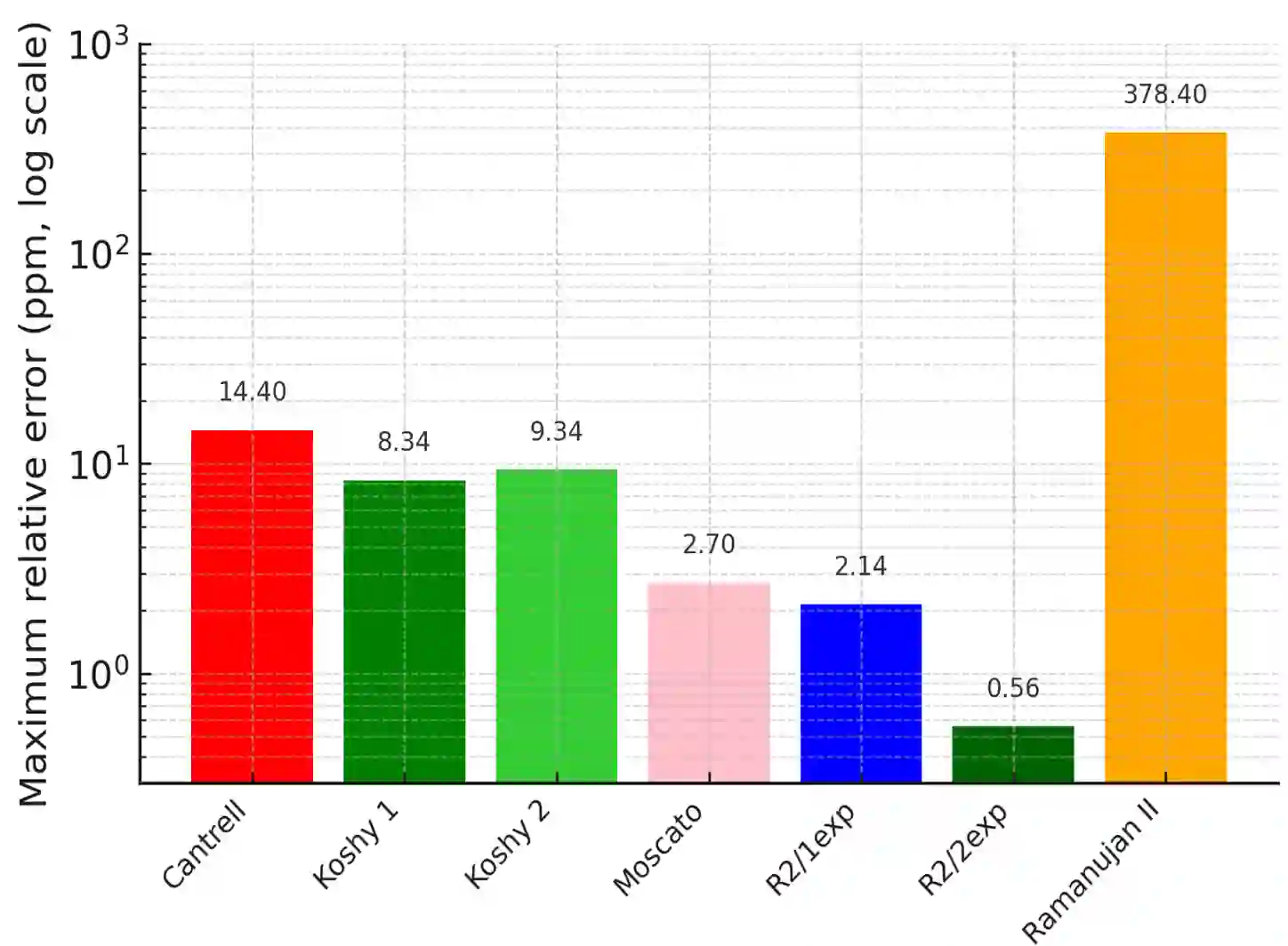
The perimeter of an ellipse has no exact closed-form expression in terms of elementary functions, and numerous approximations have been proposed since the eighteenth century. Classical formulas by Fagnano, Euler, and Ramanujan, as well as modern refinements such as Cantrell and Koshy methods, aim to reduce the approximation error while maintaining computational simplicity. In this paper, we introduce a new closed-form expression that enhances Ramanujan second formula by dividing it by 1 minus a binomial of two exponential terms resulting in a very stable approximation in a range of b/a between 1 and 1/10000, or even up to a smaller ratio. The resulting approximation remains compact, requiring only four constants, and achieving a remarkable tradeoff between simplicity and accuracy. Across the full eccentricity range of b/a in [0.0001,1], our method attains a maximum relative error of approximately 0.57 ppm with respect to the exact perimeter computed via elliptic integral. Our formula is quasi-exact at the extremes, for the circle b/a=1 and for the degenerate flat ellipse b/a=0. Compared with Cantrell approximation, the proposed method reduces the maximum relative error by a factor of 25 while preserving a short and elegant expression. This makes it one of the simplest yet most accurate closed-form and single-line approximations to the ellipse perimeter currently available in the literature.