Detection of Change Points in Piecewise Polynomial Signals Using Trend Filtering

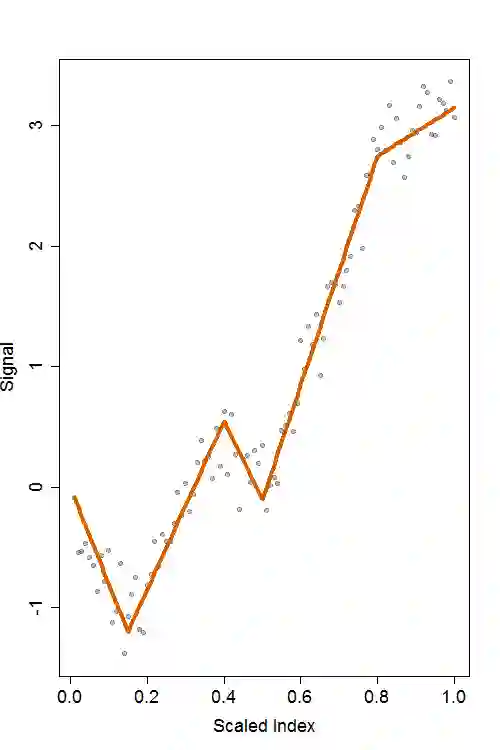
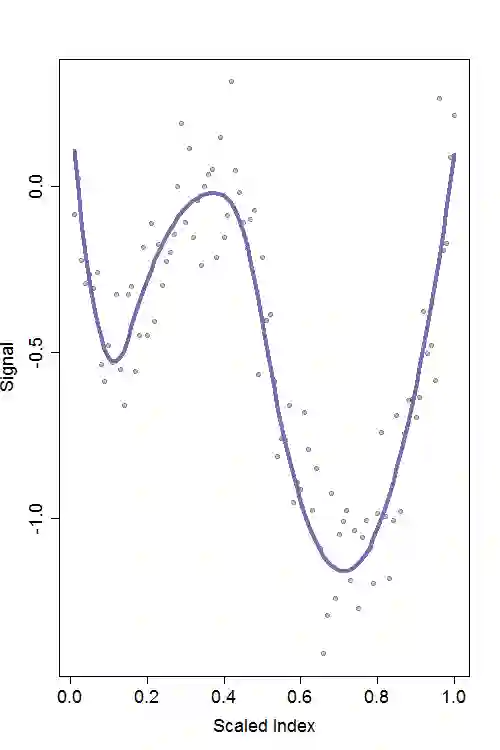
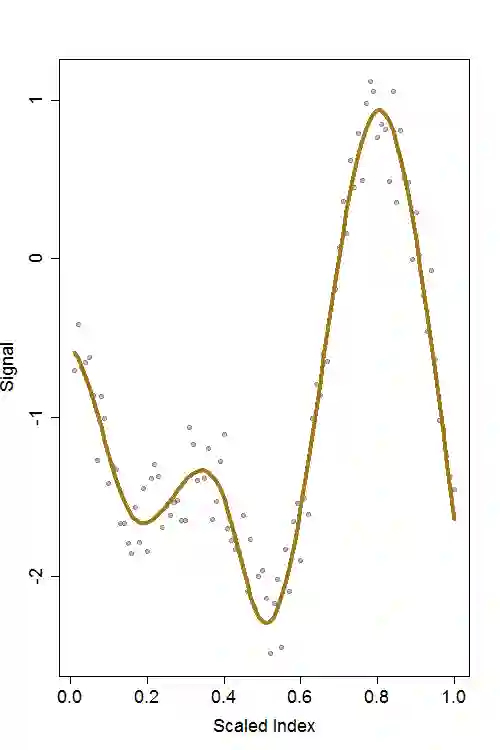
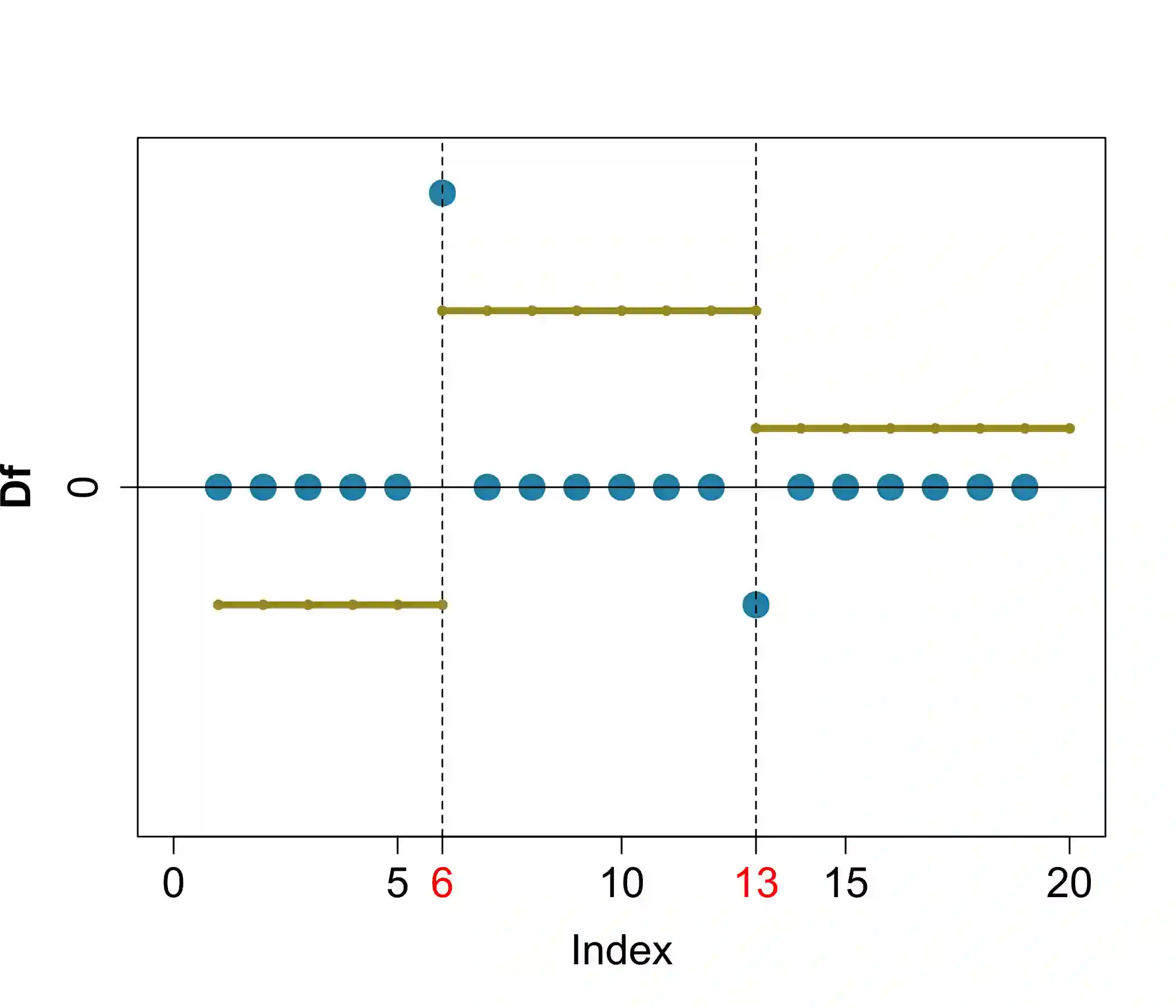
While many approaches have been proposed for discovering abrupt changes in piecewise constant signals, few methods are available to capture these changes in piecewise polynomial signals. In this paper, we propose a change point detection method, PRUTF, based on trend filtering. By providing a comprehensive dual solution path for trend filtering, PRUTF allows us to discover change points of the underlying signal for either a given value of the regularization parameter or a specific number of steps of the algorithm. We demonstrate that the dual solution path constitutes a Gaussian bridge process that enables us to derive an exact and efficient stopping rule for terminating the search algorithm. We also prove that the estimates produced by this algorithm are asymptotically consistent in pattern recovery. This result holds even in the case of staircases (consecutive change points of the same sign) in the signal. Finally, we investigate the performance of our proposed method for various signals and then compare its performance against some state-of-the-art methods in the context of change point detection. We apply our method to three real-world datasets including the UK House Price Index (HPI), the GISS surface Temperature Analysis (GISTEMP) and the Coronavirus disease (COVID-19) pandemic.