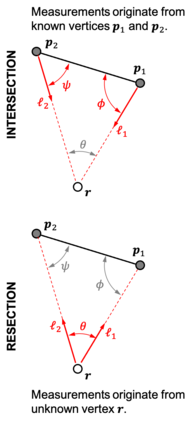
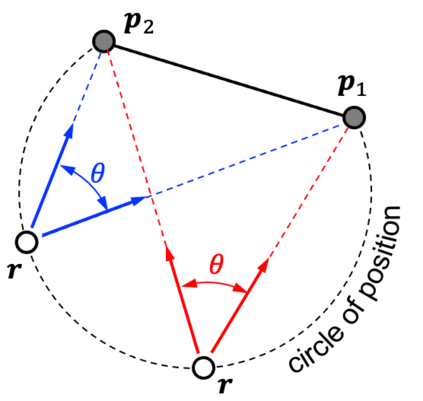
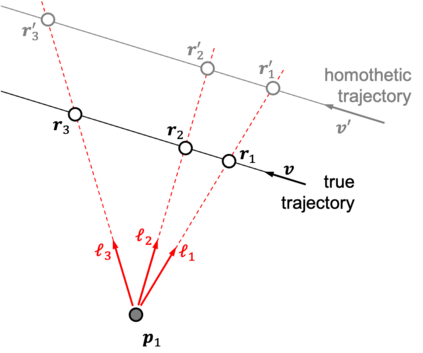
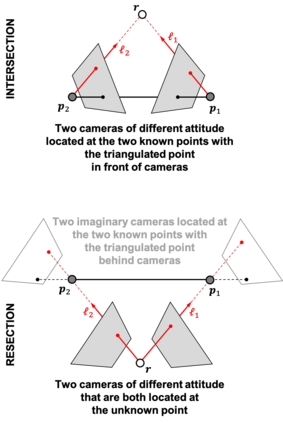
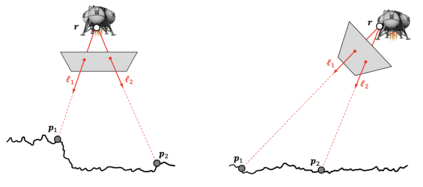
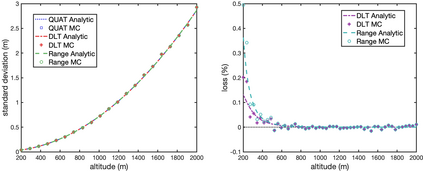
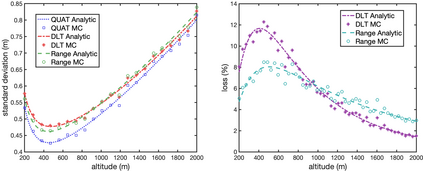
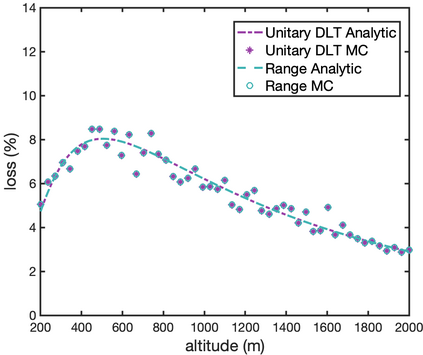
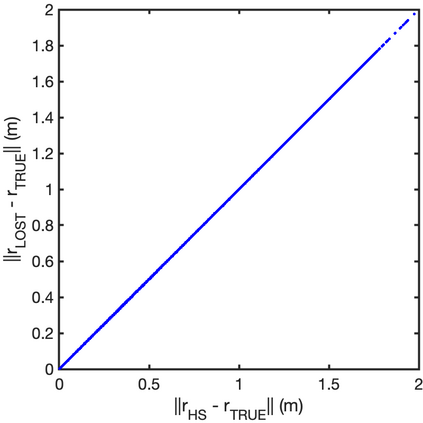
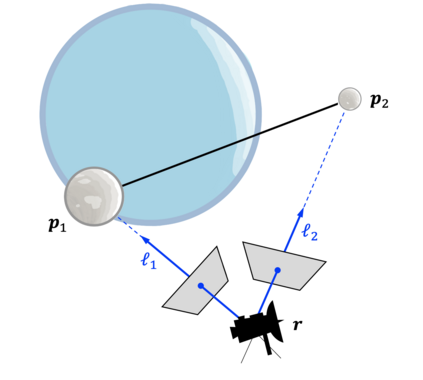
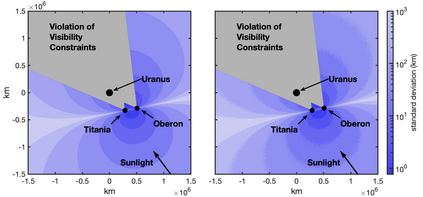
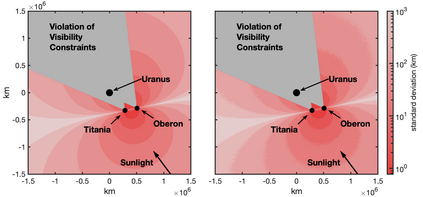
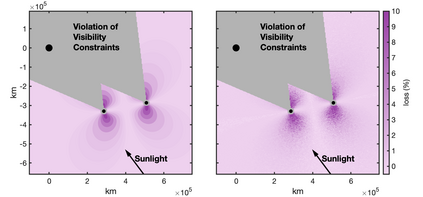
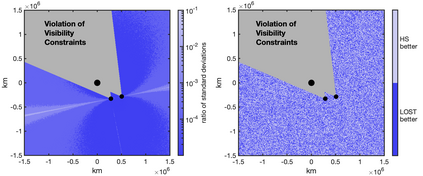
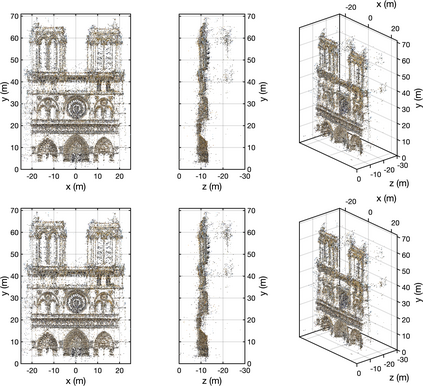
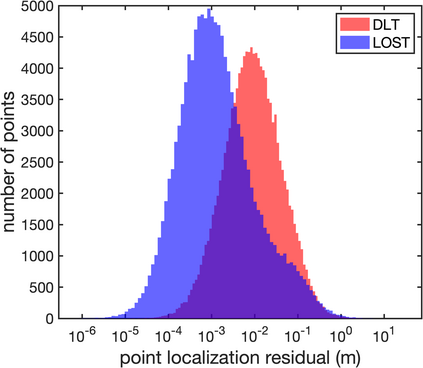
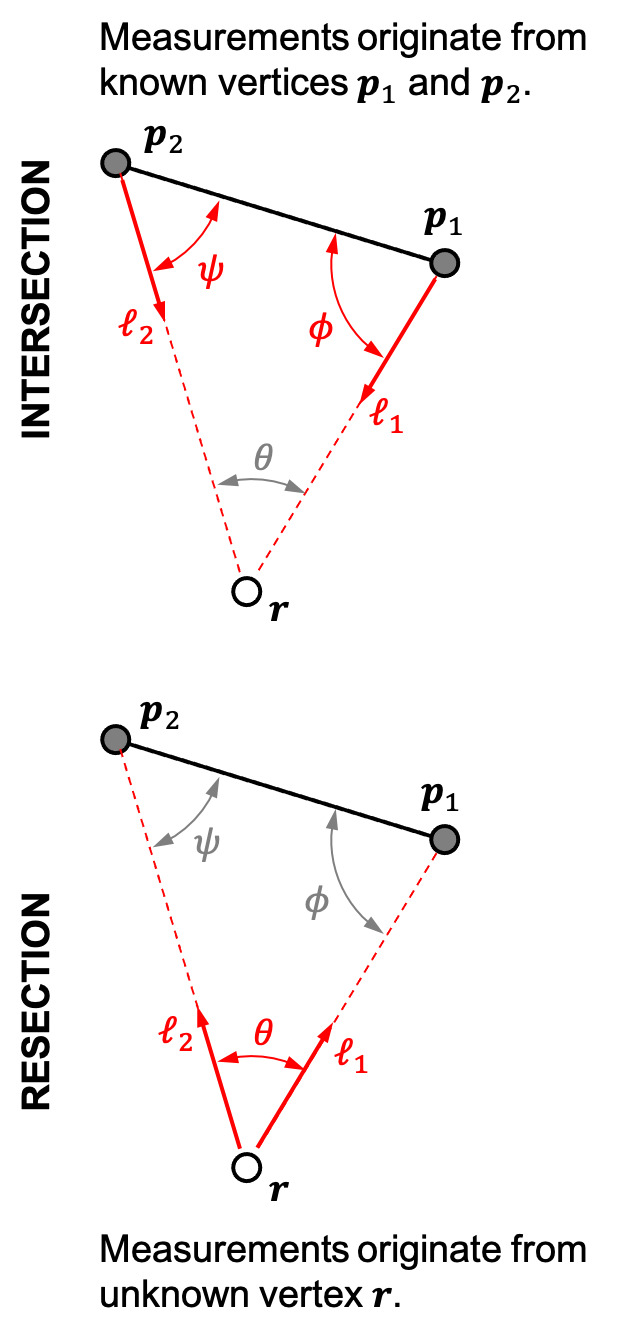
Images are an important source of information for spacecraft navigation and for three-dimensional reconstruction of observed space objects. Both of these applications take the form of a triangulation problem when the camera has a known attitude and the measurements extracted from the image are line of sight (LOS) directions. This work provides a comprehensive review of the history and theoretical foundations of triangulation. A variety of classical triangulation algorithms are reviewed, including a number of suboptimal linear methods (many LOS measurements) and the optimal method of Hartley and Sturm (only two LOS measurements). It is shown that the optimal many-measurement case may be solved without iteration as a linear system using the new Linear Optimal Sine Triangulation (LOST) method. Both LOST and the polynomial method of Hartley and Sturm provide the same result in the case of only two measurements. The various triangulation algorithms are assessed with a few numerical examples, including planetary terrain relative navigation, angles-only optical navigation at Uranus, 3-D reconstruction of Notre-Dame de Paris, and angles-only relative navigation.
翻译:这两套应用都是在照相机具有已知姿态和从图像中提取的测量数据为视线方向时出现三角测量问题。这项工作全面审查了三角测量的历史和理论基础。审查了各种经典三角算法,包括若干亚优线性线性方法(许多LS测量法)和哈特利和Sturm的最佳方法(只有两个LS测量法),这表明,最佳的多种测量情况可以在不使用新的线性最佳线性线性线性线性线性线性线性线性线性线性系统的情况下得到解决。LOST和哈特利和Sturm的多线性方法仅提供了两种测量法的相同结果。对各种三角测量算法的评估有少数数字例子,包括行星地形相对导航、乌拉努斯的角光学导航、巴黎Notre-Dame的三维再造线性线性系统以及角度相对导航。