$\mathcal{N}$IPM-HLSP: An Efficient Interior-Point Method for Hierarchical Least-Squares Programs

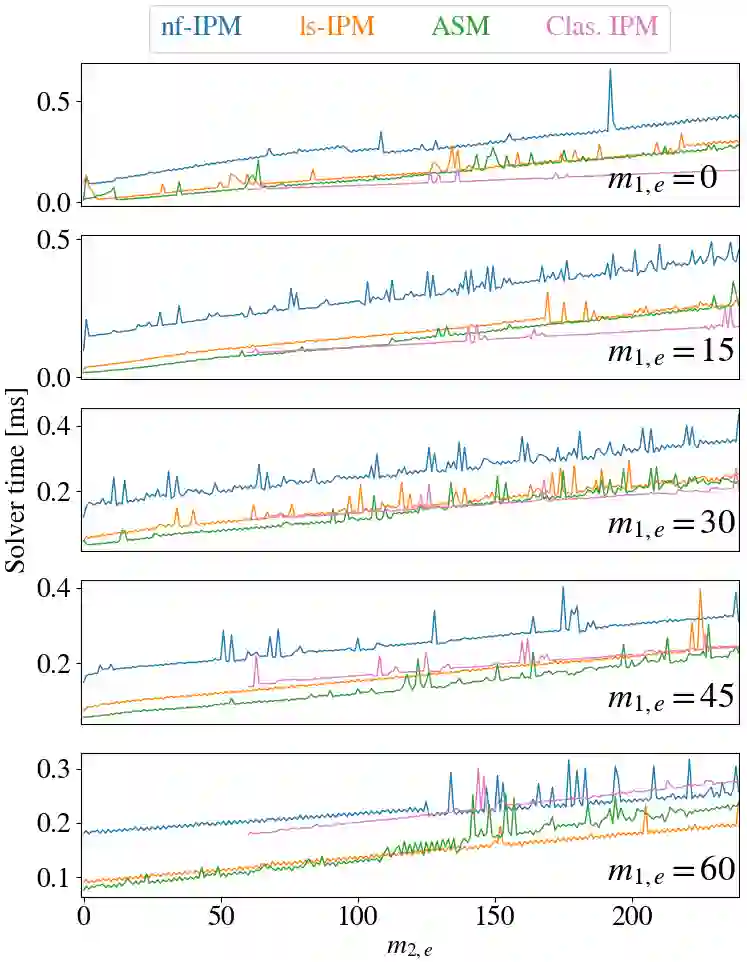
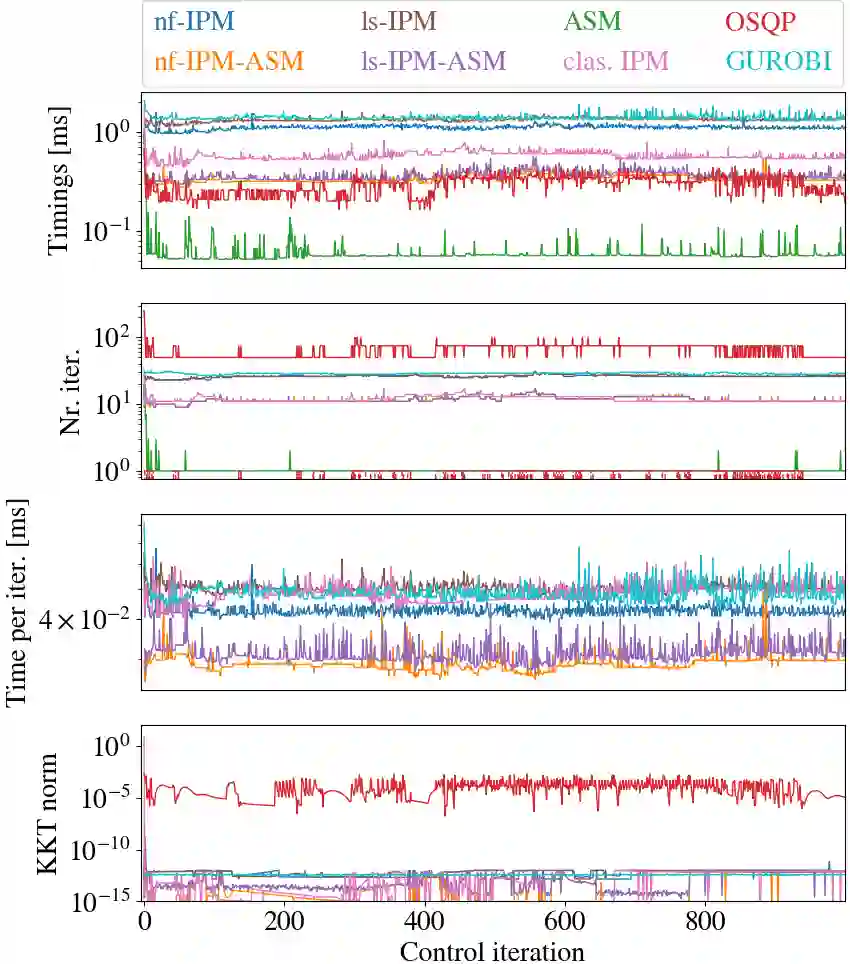
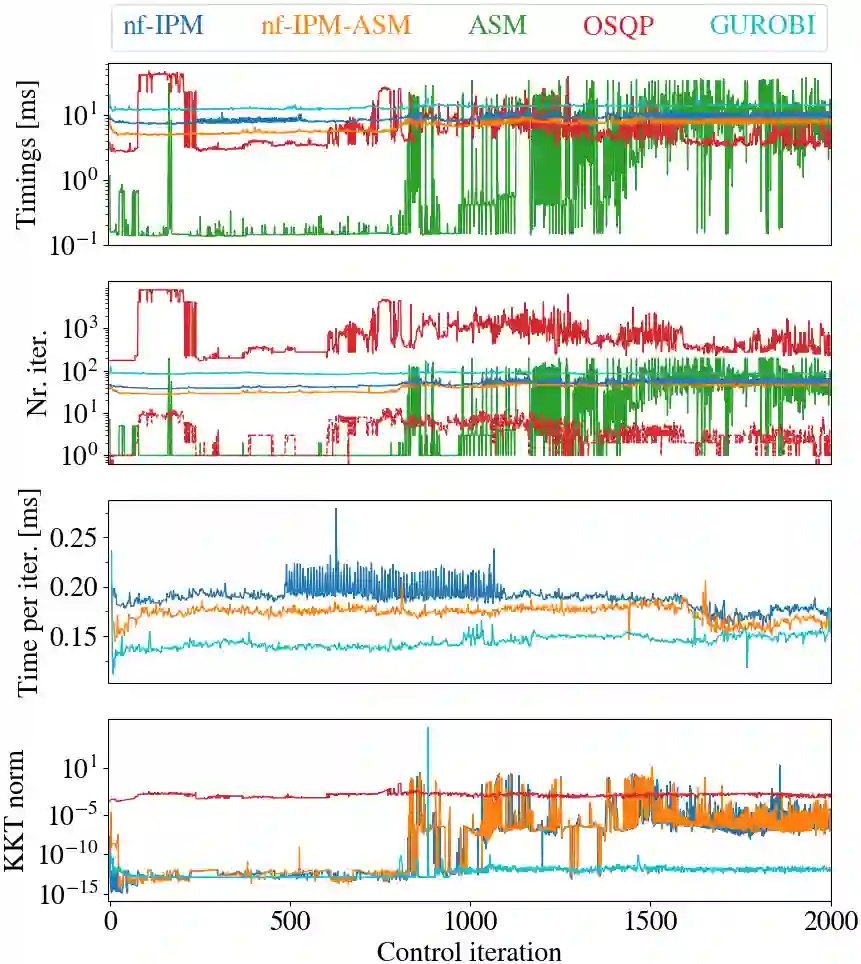
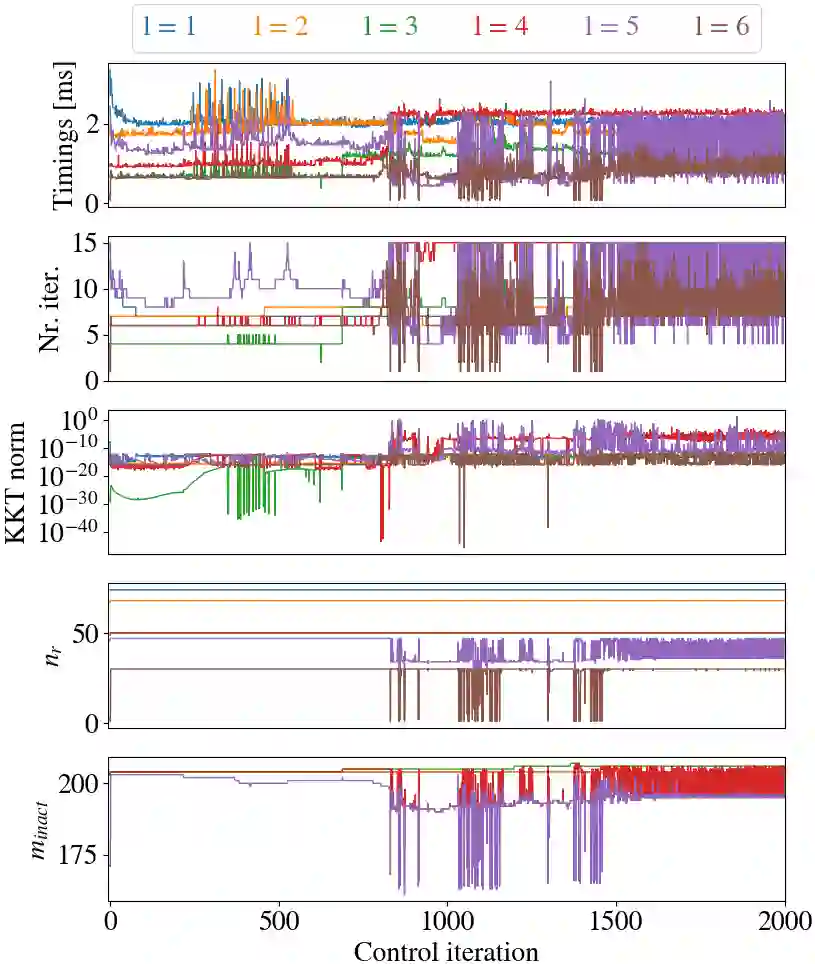
Hierarchical least-squares programs with linear constraints (HLSP) are a type of optimization problem very common in robotics. Each priority level contains an objective in least-squares form which is subject to the linear constraints of the higher priority hierarchy levels. Active-set methods (ASM) are a popular choice for solving them. However, they can perform poorly in terms of computational time if there are large changes of the active set. We therefore propose a computationally efficient primal-dual interior-point method (IPM) for HLSP's which is able to maintain constant numbers of solver iterations in these situations. We base our IPM on the null-space method which requires only a single decomposition per Newton iteration instead of two as it is the case for other IPM solvers. After a priority level has converged we compose a set of active constraints judging upon the dual and project lower priority levels into their null-space. We show that the IPM-HLSP can be expressed in least-squares form which avoids the formation of the quadratic Karush-Kuhn-Tucker (KKT) Hessian. Due to our choice of the null-space basis the IPM-HLSP is as fast as the state-of-the-art ASM-HLSP solver for equality only problems.