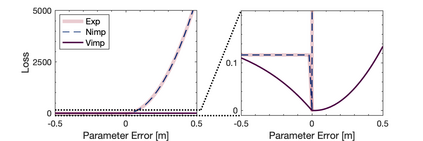
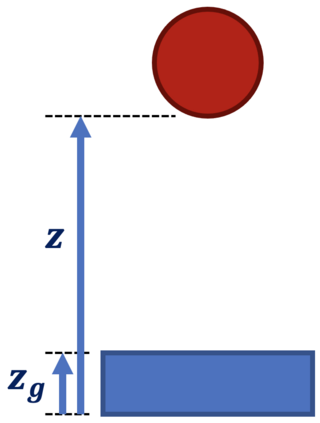
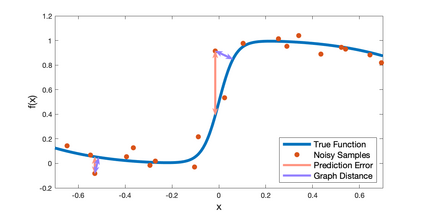
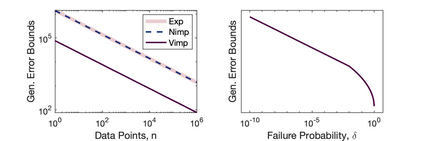
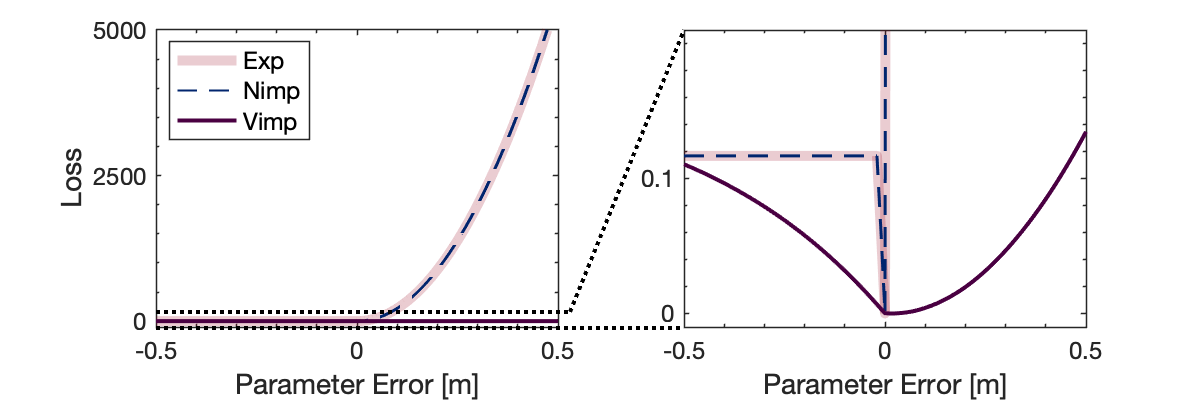
Inspired by recent strides in empirical efficacy of implicit learning in many robotics tasks, we seek to understand the theoretical benefits of implicit formulations in the face of nearly discontinuous functions, common characteristics for systems that make and break contact with the environment such as in legged locomotion and manipulation. We present and motivate three formulations for learning a function: one explicit and two implicit. We derive generalization bounds for each of these three approaches, exposing where explicit and implicit methods alike based on prediction error losses typically fail to produce tight bounds, in contrast to other implicit methods with violation-based loss definitions that can be fundamentally more robust to steep slopes. Furthermore, we demonstrate that this violation implicit loss can tightly bound graph distance, a quantity that often has physical roots and handles noise in inputs and outputs alike, instead of prediction losses which consider output noise only. Our insights into the generalizability and physical relevance of violation implicit formulations match evidence from prior works and are validated through a toy problem, inspired by rigid-contact models and referenced throughout our theoretical analysis.
翻译:受许多机器人任务中隐性学习的经验效率最近取得进步的启发,我们力求理解在几乎不连续功能面前隐性配方的理论利益,这些隐性配方是产生和中断与环境接触的系统的共同特征,如腿动动和操纵。我们提出并激励三种配方来学习一个函数:一个显性和两个隐性。我们为这三种方法中的每一种得出概括性界限,暴露出基于预测错误损失的明示和隐性方法通常不会产生紧凑的界限,而与其他基于违反性的损失定义的隐性方法相比,这些隐性配方在理论上对陡峭壁更加有力。此外,我们证明,这种违反性隐性损失可以紧紧紧的图形距离,这种距离往往具有物理根基,处理投入和产出的噪音,而不是只考虑产出噪音的预测性损失。我们对隐性配方的可概括性和实际相关性的洞察认识,与先前工作的证据相匹配,并通过一个棘手的问题加以验证,而我们理论分析通篇实论。