On the Sample Complexity of solving LWE using BKW-Style Algorithms

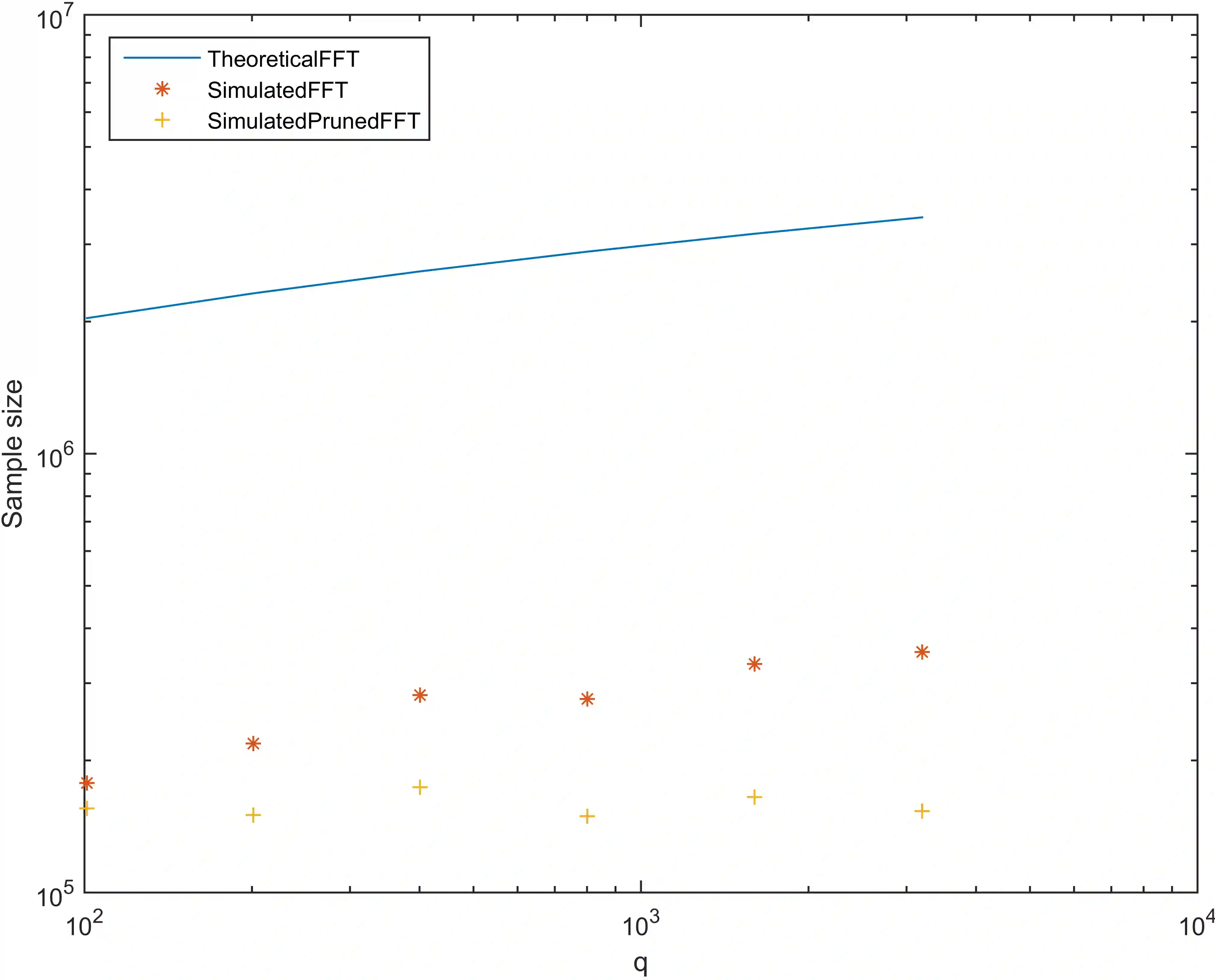
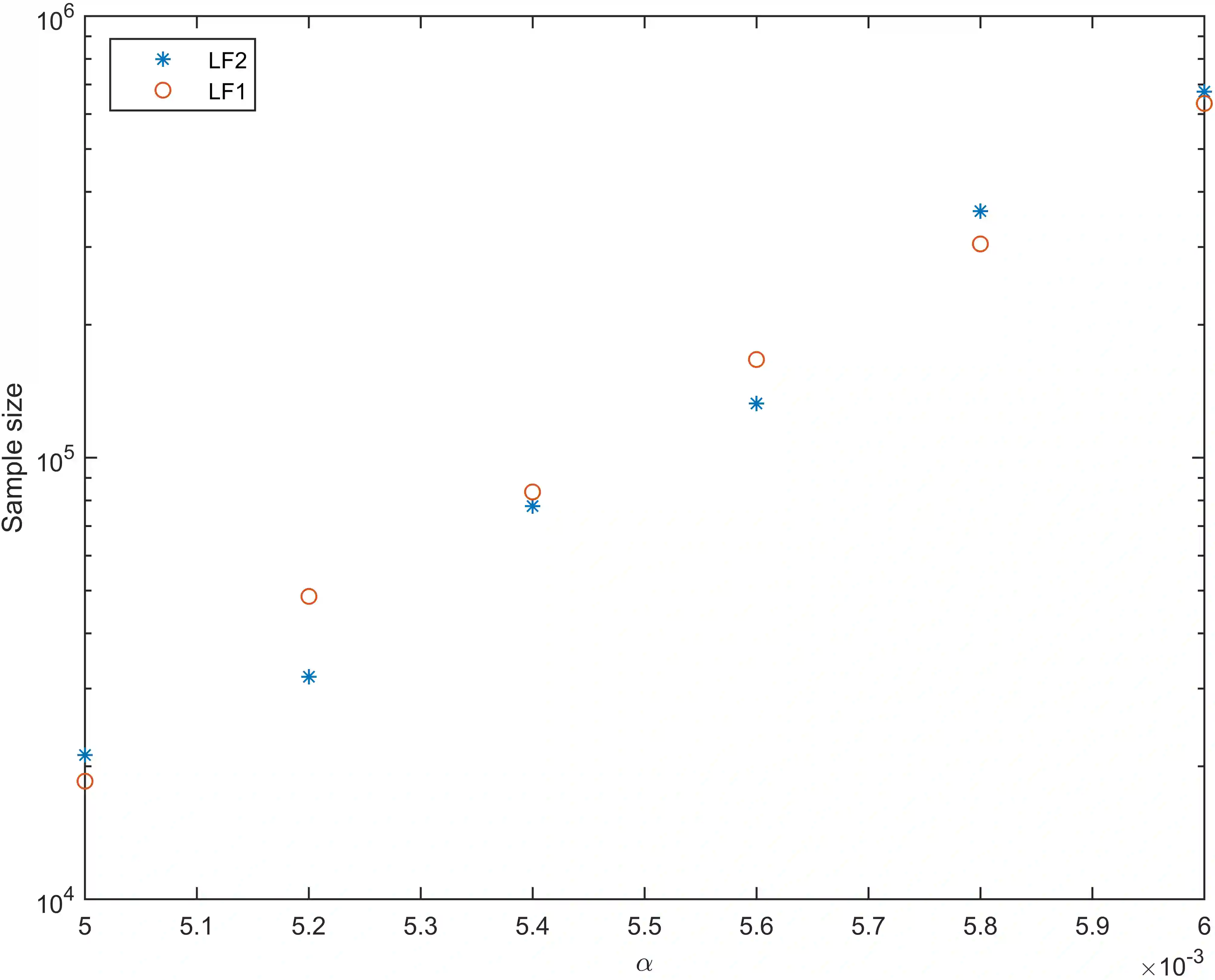
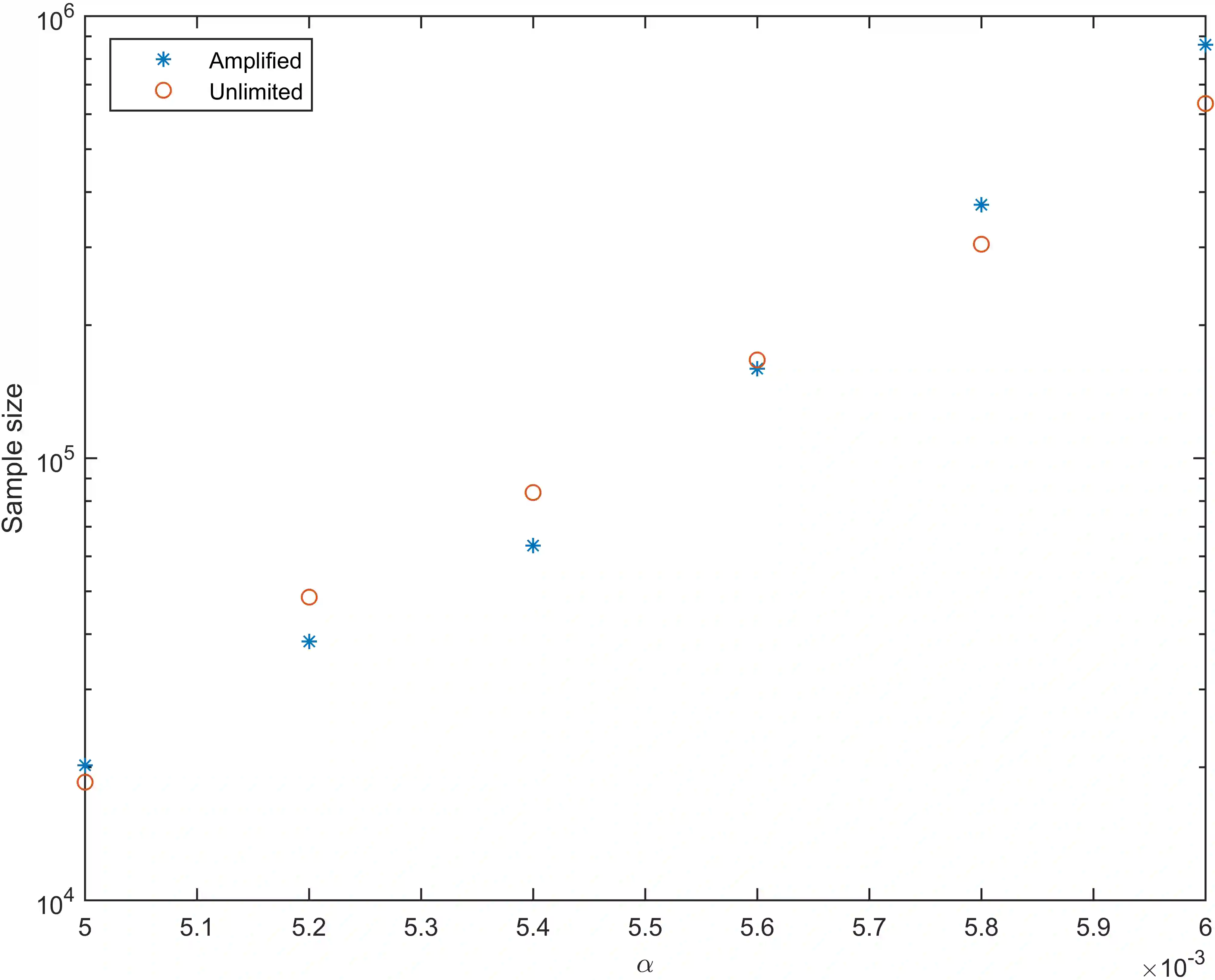
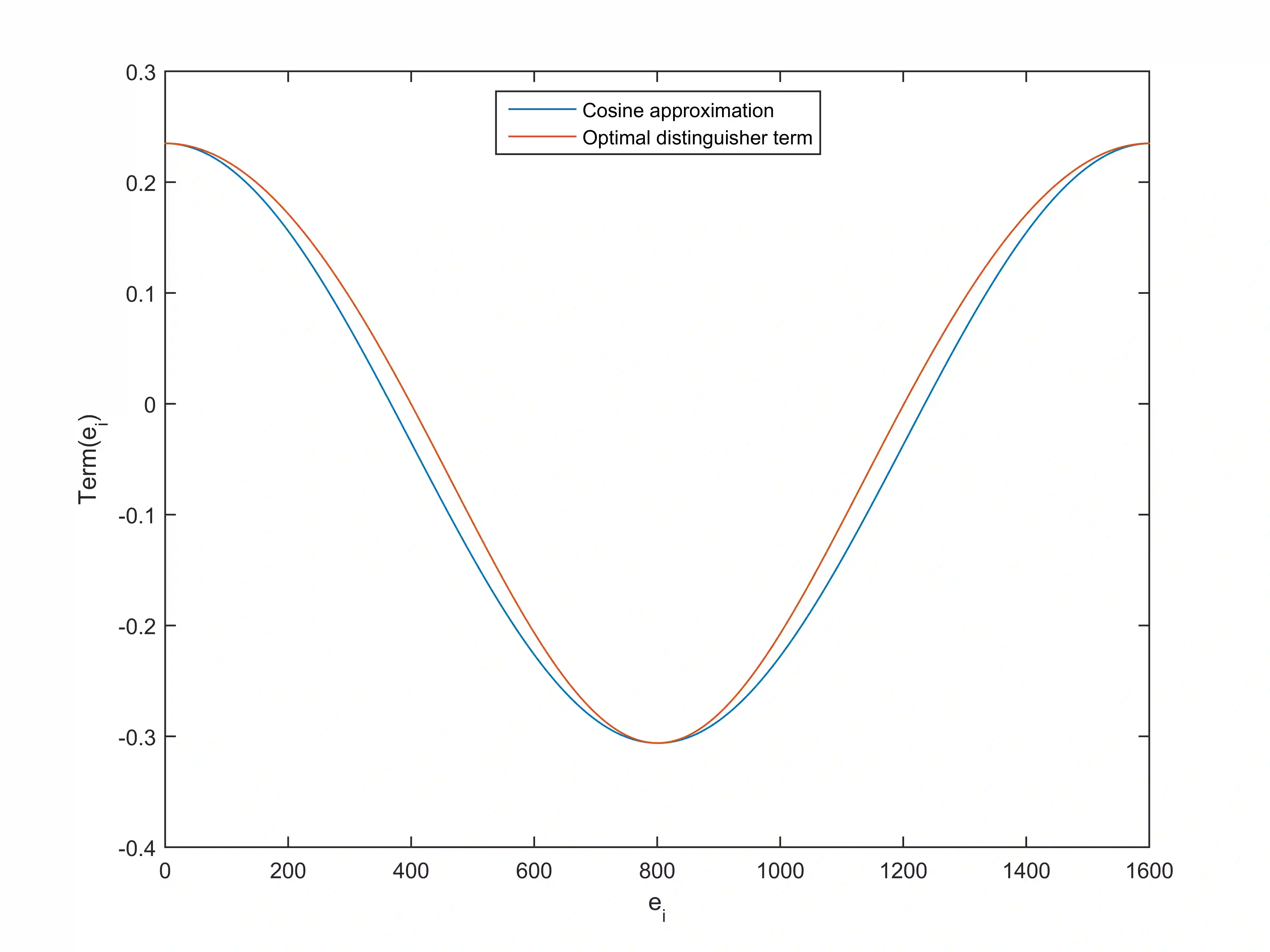
The Learning with Errors (LWE) problem receives much attention in cryptography, mainly due to its fundamental significance in post-quantum cryptography. Among its solving algorithms, the Blum-Kalai-Wasserman (BKW) algorithm, originally proposed for solving the Learning Parity with Noise (LPN) problem, performs well, especially for certain parameter settings with cryptographic importance. The BKW algorithm consists of two phases, the reduction phase and the solving phase. In this work, we study the performance of distinguishers used in the solving phase. We show that the Fast Fourier Transform (FFT) distinguisher from Eurocrypt'15 has the same sample complexity as the optimal distinguisher, when making the same number of hypotheses. We also show that it performs much better than theory predicts and introduce an improvement of it called the pruned FFT distinguisher. Finally, we indicate, via extensive experiments, that the sample dependency due to both LF2 and sample amplification is limited.