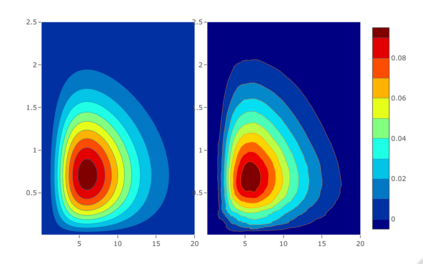
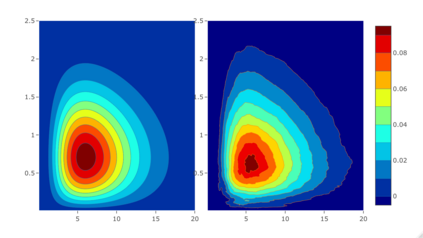
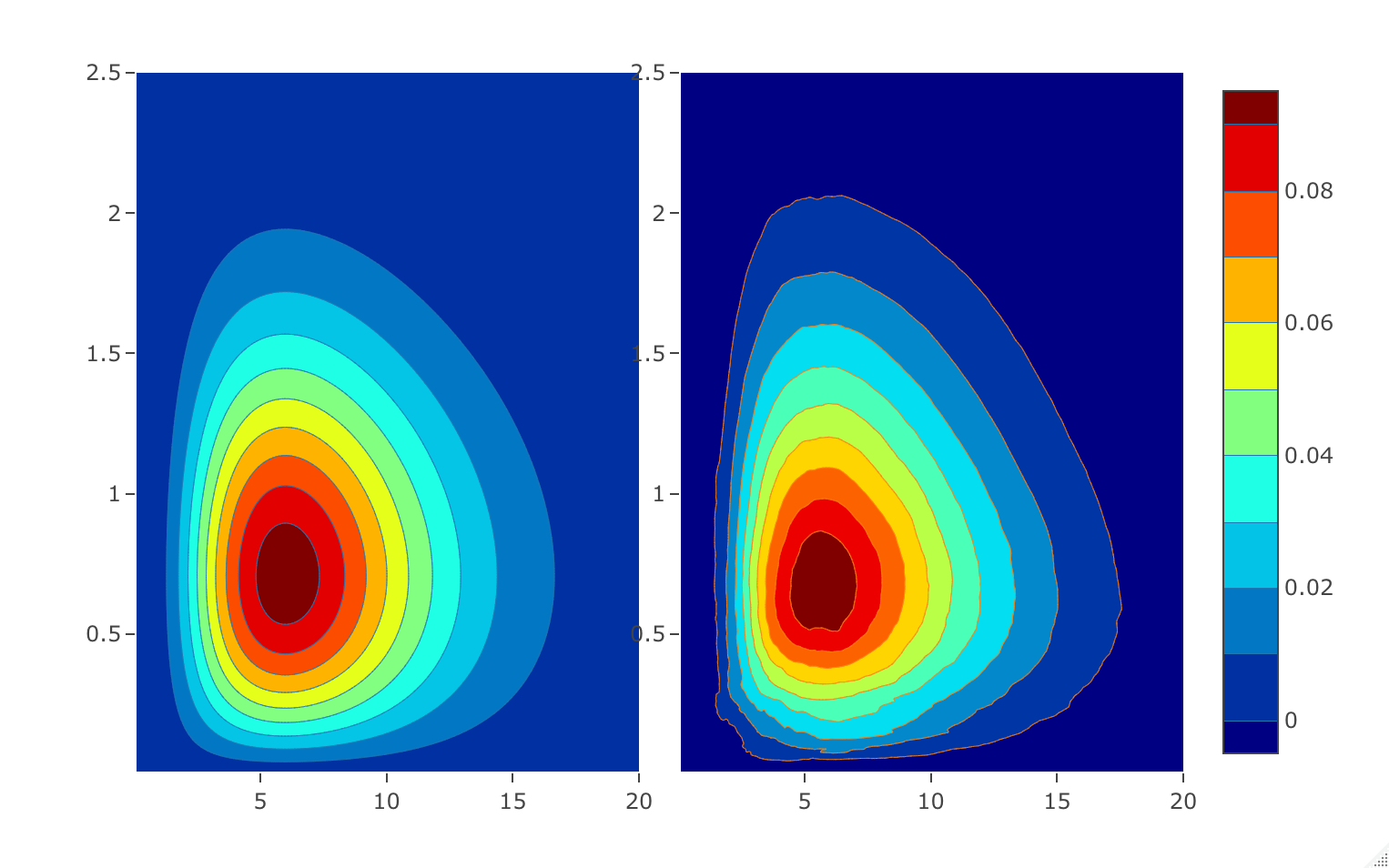
We study the non-parametric estimation of an unknown density f with support on R+^d based on an i.i.d. sample with multiplicative measurement errors. The proposed fully-data driven procedure is based on the estimation of the Mellin transform of the density f and a regularisation of the inverse of the Mellin transform by a spectral cut-off. The upcoming bias-variance trade-off is dealt with by a data-driven anisotropic choice of the cut-off parameter. In order to discuss the bias term, we consider the Mellin-Sobolev spaces which characterize the regularity of the unknown density f through the decay of its Mellin transform. Additionally, we show minimax-optimality over Mellin-Sobolev spaces of the spectral cut-off density estimator.
翻译:我们研究对未知密度的非参数估计,在 R ⁇ d 上的支持下,根据i.d. 样本进行一项具有倍增性测量误差的样本。提议的全数据驱动程序基于对Mellin 密度f 变化的估计和通过光谱截断法对Mellin 变异的反向进行常规化。即将到来的偏差偏差权衡是通过数据驱动的断点参数的反异性选择来解决。为了讨论偏差术语,我们考虑了Mellin-Sobolev 空间,该空间通过Mellin变异的衰败来描述未知密度的规律性。此外,我们展示了光谱断点密度估计仪的Mellin-Soblev 空间的微质量最佳性。