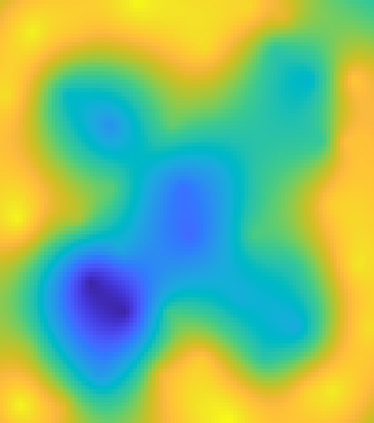
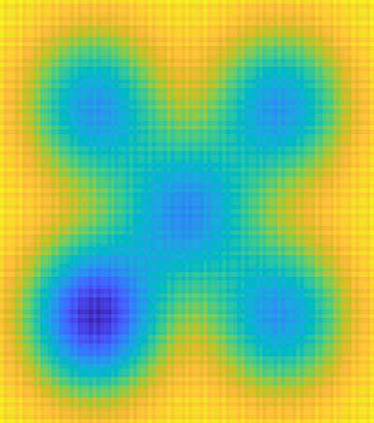
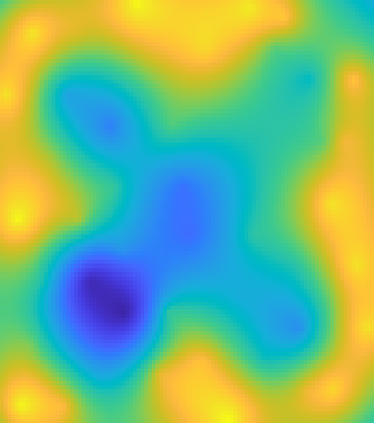
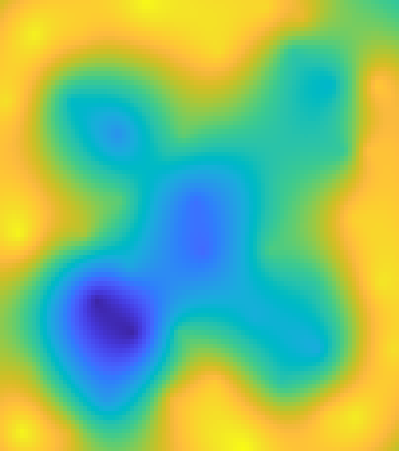
We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum. Given $n$ samples, the computational cost is $O(n^{3.5})$ in time, $O(n^2)$ in space, and we achieve a convergence rate to the global optimum that is $O(n^{-m/d + 1/2 + 3/d})$ where $m$ is the degree of differentiability of the function and $d$ the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions that have a large number of derivatives. Indeed, when $m$ is in the order of $d$, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst-case constants (that we track explicitly through the paper).
翻译:我们考虑将光滑功能仅以功能评价为基础,在全球范围内最大限度地减少光滑功能。 实现特定精确水平最佳功能评价数量的最佳功能评估的数值通常取决于明确构建功能近似值,然后通过具有指数性运行时间复杂性的算法将功能的近似值最小化; 在本文中,我们考虑采用一种方法,共同模拟该功能以近似值,并找到全球最低值。 这种方法使用无限的平平滑功能,并与多数值和方方之和等分结构有着密切的联系。 利用最近复制核心Hilbert空间的显示特性, 无限规模优化问题可以通过在功能评价数量中以时间多数值小标比值进行分校准,并在获得的最低值上以理论保证最小值为最小值。 鉴于美元样本的计算成本是美元(n%%),在空间中, 美元(n%/m/d+1/2+ 3/d}实现全球最佳度的趋同率。 美元是我们最差的数值,在最差的功能和最差值值的值中,因此, 美元的计算法阶值比值比值比值要高。