Where Have All the Kaczmarz Iterates Gone?

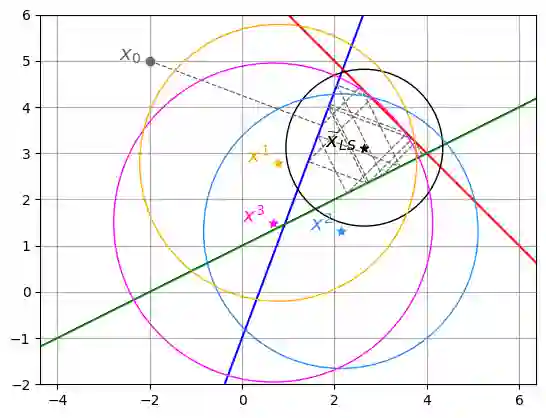
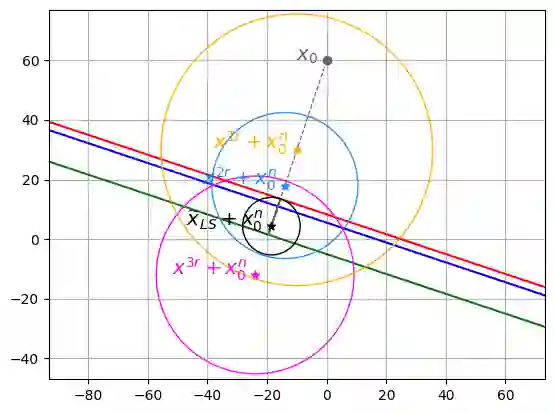
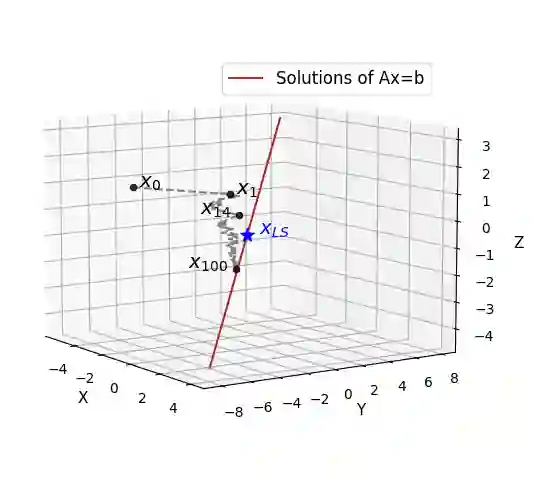
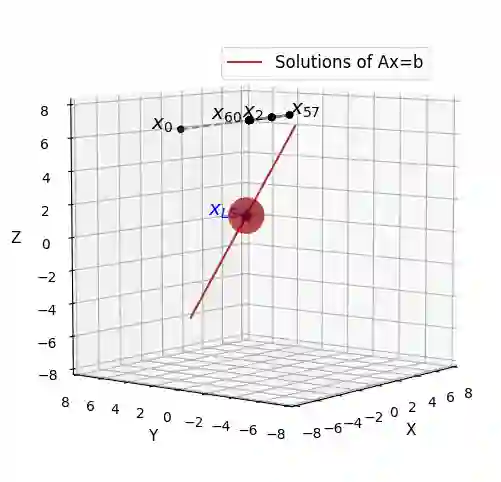
The randomized Kaczmarz (RK) algorithm is one of the most computationally and memory-efficient iterative algorithms for solving large-scale linear systems. However, practical applications often involve noisy and potentially inconsistent systems. While the convergence of RK is well understood for consistent systems, the study of RK on noisy, inconsistent linear systems is limited. This paper investigates the asymptotic behavior of RK iterates in expectation when solving noisy and inconsistent systems, addressing the locations of their limit points. We explore the roles of singular vectors of the (noisy) coefficient matrix and derive bounds on the convergence horizon, which depend on the noise levels and system characteristics. Finally, we provide extensive numerical experiments that validate our theoretical findings, offering practical insights into the algorithm's performance under realistic conditions. These results establish a deeper understanding of the RK algorithm's limitations and robustness in noisy environments, paving the way for optimized applications in real-world scientific and engineering problems.