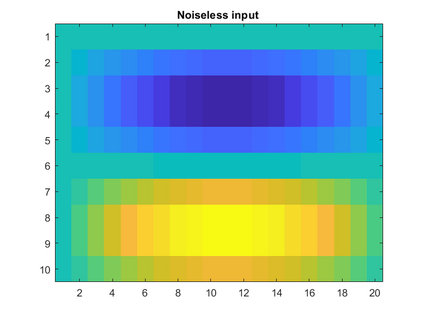
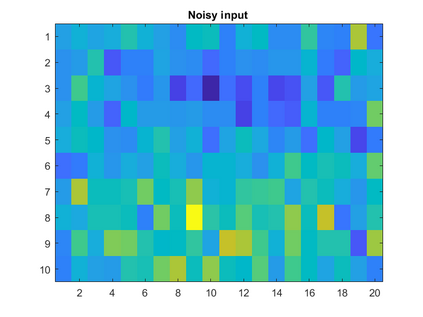
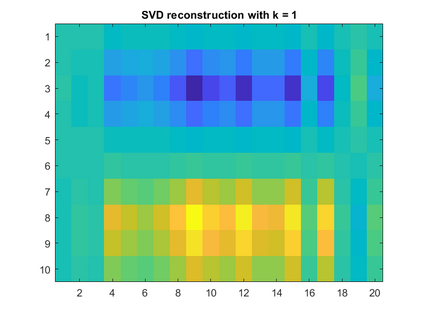
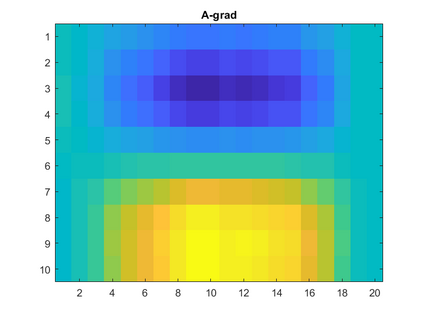
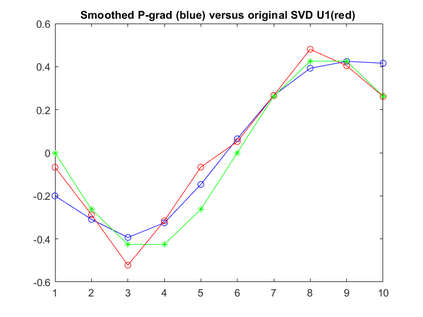
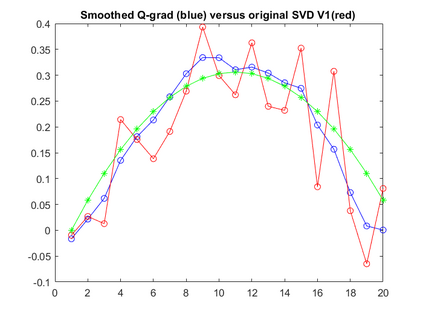
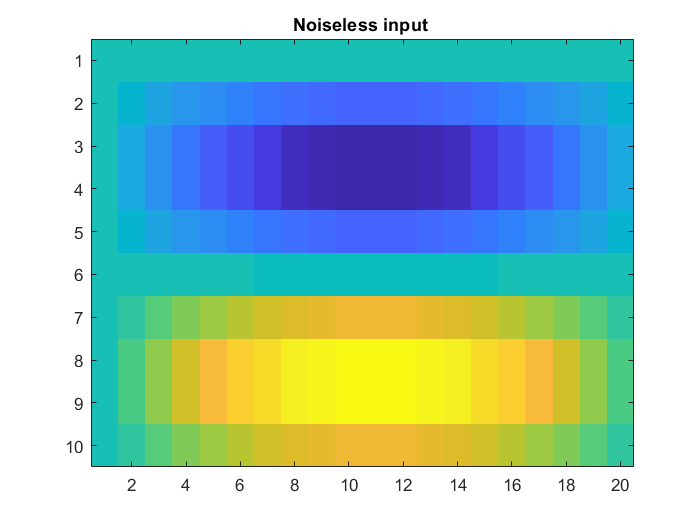
Singular Value Decomposition (SVD) and its close relative, Principal Component Analysis (PCA), are well-known linear matrix decomposition techniques that are widely used in applications such as dimension reduction and clustering. However, an important limitation of SVD/PCA is its sensitivity to noise in the input data. In this paper, we take another look at the problem of regularisation and show that different formulations of the minimisation problem lead to qualitatively different solutions.
翻译:单值分解(SVD)及其近亲属(主元件分析(PCA))是众所周知的线性矩阵分解技术,广泛用于尺寸减少和分组等应用,但是,SVD/PCA的一个重要限制是它对输入数据中的噪音的敏感度。我们在本文件中再次审视了标准化问题,并表明最小化问题的不同配方导致质量上不同的解决方案。
相关内容
专知会员服务
13+阅读 · 2020年6月10日
Arxiv
17+阅读 · 2017年12月12日